题目内容

计算：（1+
1
1×3
）×（1+
1
2×4
）×（1+
1
3×5
）×（1+
1
4×6
）×（1+
1
5×7
）×（1+
1
6×8
）×（1+
1
7×9
）×（1+
1
8×10
）×（1+
1
9×11
）×（1+
1
10×12
）×（1+
1
11×13
）．
考点：有理数的混合运算
专题：
分析：根据有理数混合运算的法则进行计算即可．
解答：解：原式=（1+
1
3
）×（1+
1
8
）×（1+
1
15
）×（1+
1
24
）×（1+
1
35
）×（1+
1
48
）×（1+
1
63
）×（1+
1
80
）×（1+
1
99
）×（1+
1
120
）×（1+
1
143
）
=
4
3
×
9
8
×
16
15
×
25
24
×
36
35
×
49
48
×
64
63
×
81
80
×
100
99
×
121
120
×
144
143

=
3
2
×
16
15
×
25
24
×
36
35
×
49
48
×
64
63
×
81
80
×
100
99
×
121
120
×
144
143

=
8
5
×
25
24
×
36
35
×
49
48
×
64
63
×
81
80
×
100
99
×
121
120
×
144
143

=
5
3
×
36
35
×
49
48
×
64
63
×
81
80
×
100
99
×
121
120
×
144
143

=
12
7
×
49
48
×
64
63
×
81
80
×
100
99
×
121
120
×
144
143

=
7
4
×
64
63
×
81
80
×
100
99
×
121
120
×
144
143

=
16
9
×
81
80
×
100
99
×
121
120
×
144
143

=
9
5
×
100
99
×
121
120
×
144
143

=
20
11
×
121
120
×
144
143

=
11
6
×
144
143

=
14
13
．
点评：本题考查的是有理数的混合运算，熟知有理数混合运算的顺序是解答此题的关键．
练习册系列答案
相关题目
已知∠1的余角是∠2的补角的
1
3
，并且∠2=
3
2
∠1，求∠1+∠2的度数．
某班级前年暑假将勤工俭学挣得的班费中的4000元，按一年定期存入银行，去年暑假，到期后取出来1000元捐给希望工程，将剩下的3000元，与利息继续按一年定期存入该银行，待今年暑假毕业时全部捐给母校，若该银行今年利率无变化，且今年暑假到期后可取得本息共3360元．该银行一年定期存款的年利率是多少？
解方程：
0.07-0.01x
0.04
-
10x-10
30
=x+1．
计算：
（1）-（-0.252）÷[3.5-（-1+3
1
4
）]×
2
5
；
（2）（-27
9
11
）÷9-（
1
2
+
2
3
-
3
4
-
11
12
）×（-24）．
计算（x-1-
8
x+1
）÷
x+3
x+1
，并求当x=4时的值．
老师布置了一道作业题；当a为何值时，分式
a-1
a2-1
无意义？小刚的解法如下；
a-1
a2
=
a-1
(a-1)(a+1)
．由a+1=0得，a=-1，所以当a=-1时，分式无意义，小刚的解法是否正确？若有错，请你找出错误的原因并改正．
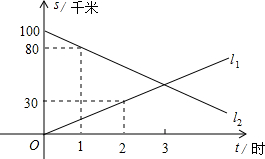A、B两地相距100千米，甲、乙两人骑自行车同时分别从A、B两地相向而行．假设它们都保持匀速行驶，则他们各自到A地的距离S（千米）都是骑车时间t（时）的一次函数图象（如图所示）．请你根据图象所提供的信息，利用所学函数知识解答下列问题：
（1）经过多长时间，甲到达B地？
（2）经过多长时间，乙到达A地？
（3）经过多长时间甲、乙两人相遇？
若等腰△ABC顶角为∠A，底边长BC=a，底边上的高为h，若90°≤∠A≤120°，h=1，则a的取值范围是（　　）
A、
2
≤a≤2
B、2
2
≤a≤4
C、1≤a≤
3
D、2≤a≤2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网