题目内容
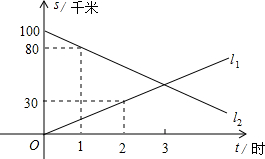A、B两地相距100千米，甲、乙两人骑自行车同时分别从A、B两地相向而行．假设它们都保持匀速行驶，则他们各自到A地的距离S（千米）都是骑车时间t（时）的一次函数图象（如图所示）．请你根据图象所提供的信息，利用所学函数知识解答下列问题：（1）经过多长时间，甲到达B地？
（2）经过多长时间，乙到达A地？
（3）经过多长时间甲、乙两人相遇？
考点：一次函数的应用
专题：
分析：（1）利用待定系数法求得函数甲的解析式，然后令y=100即可求得x的值；
（2）利用待定系数法求得函数的解析式，然后令y=0求得x即可；
（3）根据（1）（2）求得函数解析式，当两个y相等时，求得x即可．
（2）利用待定系数法求得函数的解析式，然后令y=0求得x即可；
（3）根据（1）（2）求得函数解析式，当两个y相等时，求得x即可．
解答：解：（1）设甲的函数解析式是y=kx，
根据题意得：2k=30，
解得：k=15，
则甲的函数解析式是y=15x，
当y=100时，则15x=100，
解得：x=
，
则经过
小时甲到达B地；
（2）设乙的函数解析式是：y=mx+n，根据题意得：
，
解得：
，
则函数的解析式是：y=-20x+100．
当y=0时，-20x+100=0，解得：x=5，
则经过5小时乙到达A地；
（3）根据题意得：15x=-20x+100，
解得：x=
，
则经过
小时，两人相遇．
根据题意得：2k=30，
解得：k=15，
则甲的函数解析式是y=15x，
当y=100时，则15x=100，
解得：x=
| 20 |
| 3 |
则经过
| 20 |
| 3 |
（2）设乙的函数解析式是：y=mx+n，根据题意得：
|
解得：
|
则函数的解析式是：y=-20x+100．
当y=0时，-20x+100=0，解得：x=5，
则经过5小时乙到达A地；
（3）根据题意得：15x=-20x+100，
解得：x=
| 20 |
| 7 |
则经过
| 20 |
| 7 |
点评：本题考查了待定系数法求函数的解析式，理解题目中x和y表示的实际意义是本题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，线段OA与OA′关于一、三象限的角平分线对称，已知点A的坐标为（2，1），则点A′的坐标为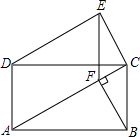
如图，四边形ABCD是矩形，∠EDC=∠CAB，∠DEC=90°，过点B作BF⊥AC于点F，连结EF，求证：
