题目内容
6.(1)计算:(-2)2+($\sqrt{3}$-π)0+|1-$\sqrt{3}$|;(2)解方程组:$\left\{\begin{array}{l}{2x+y=1}\\{x-2y=3}\end{array}\right.$.
分析 (1)原式第一项利用乘方的意义计算,第二项利用零指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)原式=4+1+$\sqrt{3}$-1=4+$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{2x+y=1①}\\{x-2y=3②}\end{array}\right.$,
①×2+②,得5x=5,即x=1,
将x=1代入①,得y=-1,
则原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
点评 此题考查了实数的运算,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
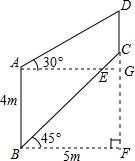 某大型机器零件的形状如图所示,已知AB∥DC,AE∥BF,根据图中数据,计算CD的长度(精确到十分位)
某大型机器零件的形状如图所示,已知AB∥DC,AE∥BF,根据图中数据,计算CD的长度(精确到十分位)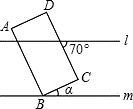 如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=20度.
如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=20度.