题目内容
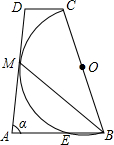 如图,在梯形ABCD中,AB∥CD,AD=BC,底角为a,以腰BC为直径作圆,与另一腰切于点M,交较长底边AB于点E,则
如图,在梯形ABCD中,AB∥CD,AD=BC,底角为a,以腰BC为直径作圆,与另一腰切于点M,交较长底边AB于点E,则| BE |
| AE |
考点:切线的性质
专题:计算题
分析:作EH⊥AD于H,连结OM、CE、OE,如图,设⊙O的半径为R,根据圆周角定理得到∠CEB=90°,再根据切线的性质得OM⊥AD,接着根据等腰梯形的性质得∠ABC=∠A=α,由于∠OEB=∠B=α,则∠OEB=∠A,所以OE∥AD,于是可判断四边形OMHE为正方形,得到HE=OE=R,根据锐角三角函数的定义,在Rt△AEH中得到AE=
,在Rt△BCE中得到BE=2Rcosα,然后计算
的值.
| R |
| sinα |
| BE |
| AE |
解答:解:作EH⊥AD于H,连结OM、CE、OE,如图,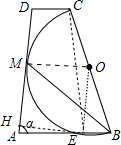 设⊙O的半径为R,
设⊙O的半径为R,
∵BC为直径,
∴∠CEB=90°,
∵AD为⊙O的切线,
∴OM⊥AD,
∵AB∥CD,AD=BC,
∴∠ABC=∠A=α,
∵OB=OE,
∴∠OEB=∠B=α,
∴∠OEB=∠A,
∴OE∥AD,
∴四边形OMHE为矩形,
而OM=OE,
∴四边形OMHE为正方形,
∴HE=OE=R,
在Rt△AEH中,∵sinA=
,
∴AE=
,
在Rt△BCE中,∵cosB=
,
∴BE=2Rcosα,
∴
=
=2sinαcosα.
故答案为2sinαcosα.
 设⊙O的半径为R,
设⊙O的半径为R,∵BC为直径,
∴∠CEB=90°,
∵AD为⊙O的切线,
∴OM⊥AD,
∵AB∥CD,AD=BC,
∴∠ABC=∠A=α,
∵OB=OE,
∴∠OEB=∠B=α,
∴∠OEB=∠A,
∴OE∥AD,
∴四边形OMHE为矩形,
而OM=OE,
∴四边形OMHE为正方形,
∴HE=OE=R,
在Rt△AEH中,∵sinA=
| HE |
| AE |
∴AE=
| R |
| sinα |
在Rt△BCE中,∵cosB=
| BE |
| BC |
∴BE=2Rcosα,
∴
| BE |
| AE |
| 2Rcosα | ||
|
故答案为2sinαcosα.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.合理构造直角三角形,应用锐角三角函数的定义进行计算是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
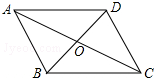 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )| A、17 | B、27 | C、34 | D、44 |
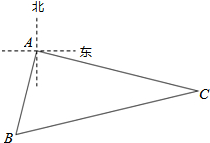 如图,轮船从港口A出发,沿着南偏西15°的方向航行了100海里到达B处,沿着北偏东75°的方向航行200海里到达了C处.
如图,轮船从港口A出发,沿着南偏西15°的方向航行了100海里到达B处,沿着北偏东75°的方向航行200海里到达了C处.
 如图,把一个三角板绕直角顶点A转动一定的角度,若∠BAE=127°,则∠DAC=
如图,把一个三角板绕直角顶点A转动一定的角度,若∠BAE=127°,则∠DAC=