题目内容
4. 如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )| A. | 5cm | B. | 8cm | C. | 10cm | D. | 12cm |
分析 设光盘的圆心为O,过点O作OA垂直直尺于点A,连接OB,再设OB=r,利用勾股定理求出r的值即可.
解答 解:设光盘的圆心为O,如图所示:
过点O作OA垂直直尺于点A,连接OB,设OB=r,
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,
∴AB=$\frac{1}{2}$×(10-2)=4,
∵刻度尺宽2cm,
∴OA=r-2,
在Rt△OAB中,
OA2+AB2=OB2,即(r-2)2+42=r2,
解得:r=5.
∴该光盘的直径是10cm.
故选:C.
点评 本题考查的是垂径定理的应用勾股定理;根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目

 解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中.
解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中. 如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=5,则△BCE的面积为5.
如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=5,则△BCE的面积为5.
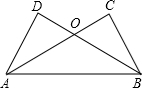 如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,若AC=5,BO=3,则OD=2.
如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,若AC=5,BO=3,则OD=2. 小张手机月基本费用为18元,某月,他把手机费中各项费用的情况制成扇形统计图(如图),则他该月的基本话费为90元.
小张手机月基本费用为18元,某月,他把手机费中各项费用的情况制成扇形统计图(如图),则他该月的基本话费为90元.