��Ŀ����
15����1����ͼ��1���ڡ�ABC�У���ACB=2��B����C=90�㣬ADΪ��BAC��ƽ�߽�BC��D����֤��AB=AC+CD������ʾ����AB�Ͻ�ȡAE=AC������DE����2����ͼ��2������C��90��ʱ�������������䣬�߶�AB��AC��CD����������������ϵ��ֱ��д�����������Ҫ֤����
��3����ͼ��3������ACB��90�㣬ADΪ��ABC����ǡ�CAF��ƽ���ߣ���BC���ӳ����ڵ�D�����߶� AB��AC��CD����������������ϵ��д����IJ��룬������֤����

���� ��1����AB�Ͻ�ȡAE=AC������DE�����ݽ�ƽ���ߵĶ���õ���1=��2���Ƴ���ACD�ա�AED��SAS��������ȫ�������ε����ʵõ���AED=��C=90��CD=ED��������֪�����õ���B=45�㣮��á�EDB=��B=45�㣮�õ�DE=BE�����������õ�CD=BE�����ɵõ����ۣ�
��2����ACȡһ��EʹAB=AE������DE����֤��ABD�ա�AED�����ԡ�B=��AED��BD=DE������Ϊ��B=2��C�����ԡ�AED=2��C����Ϊ��AED�ǡ�EDC����ǣ����ԡ�EDC=��C������ED=EC��BD=EC��������֤��AB+BD=AE+EC=AC��
��3����AB���ӳ���AF��ȡһ��E��ʹ��AE=AC������DE��֤����ACD�ա�AED������ȫ�������ε����ʵõ�DE=BE��BE=CD�����ɵó����ۣ�
���  �⣺��1����ͼ1��ʾ����AB�Ͻ�ȡAE=AC������DE��
�⣺��1����ͼ1��ʾ����AB�Ͻ�ȡAE=AC������DE��
��ADƽ�֡�BAC��
���1=��2��
�ڡ�ACD�͡�AED�У�
$\left\{\begin{array}{l}{AC=AE}\\{��1=��2}\\{AD=AD}\end{array}\right.$��
���ACD�ա�AED��SAS����
���AED=��C=90��CD=ED��
�֡ߡ�ACB=2��B����C=90�㣬
���B=45�㣮
���EDB=��B=45�㣮
��DE=BE��
��CD=BE��
��AB=AE+BE��
��AB=AC+CD��
��2��֤������ABȡһ��EʹAC=AE��
�ڡ�ACD�͡�AED�У�
$\left\{\begin{array}{l}{AC=AE}\\{��BAD=��EAD}\\{AD=AD}\end{array}\right.$��
���ACD�ա�AED��
���C=��AED��CD=DE��
�֡ߡ�C=2��B��
���AED=2��B��
�ߡ�AED�ǡ�EDC����ǣ�
���EDB=��B��
��ED=EB��
��CD=EB��
��AB=AC+CD��
��3��AB=CD-AC
֤������BA���ӳ���AF��ȡһ��E��ʹ��AE=AC������DE��
�ڡ�ACD�͡�AED�У�
$\left\{\begin{array}{l}{AC=AE}\\{��CAD=��EAD}\\{AD=AD}\end{array}\right.$��
���ACD�ա�AED��SAS����
���ACD=��AED��CD=DE��
���ACB=��FED��
�֡ߡ�ACB=2��B��
���FED=2��B��
�֡ߡ�FED=��B+��EDB��
���EDB=��B��
��DE=BE��
��BE=CD��
��AB=CD-AC��
���� ���⿼����ȫ�������ε��ж������ʣ����������ε��ж������ʣ����������߹����ȫ���������ǽ���Ĺؼ���Ҳ�DZ�����ѵ㣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | ax2-ax=x��ax-a�� | B�� | a2b2+ab2c+b2=b2��a2+ac+1�� | ||
| C�� | x2-y2=��x-y��2 | D�� | x2-5x-6=��x-2����x-3�� |
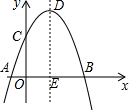 ��ͼ����ƽ��ֱ������ϵ�У���֪��������x�ύ�ڵ�A��-1��0���͵�B����y�ύ�ڵ�C��0��2�����Գ���Ϊֱ��x=1���Գ��ύx���ڵ�E��
��ͼ����ƽ��ֱ������ϵ�У���֪��������x�ύ�ڵ�A��-1��0���͵�B����y�ύ�ڵ�C��0��2�����Գ���Ϊֱ��x=1���Գ��ύx���ڵ�E�� ��ͼ����֪��ABC�����������ڸ���ϣ�
��ͼ����֪��ABC�����������ڸ���ϣ� ��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CDB=30�㣬CD=2$\sqrt{3}$������Ӱ���ֵ����Ϊ$\frac{2��}{3}$��
��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CDB=30�㣬CD=2$\sqrt{3}$������Ӱ���ֵ����Ϊ$\frac{2��}{3}$�� ��ͼ����һ������Ϊ2cm�Ŀ̶ȳ���Բ�ι������ƶ������̶ȳߵ�һ�����������ʱ����һ������̱�Ե�������㴦�Ķ���ǡ���ǡ�2���͡�10������λ��cm������ô���̵�ֱ���ǣ�������
��ͼ����һ������Ϊ2cm�Ŀ̶ȳ���Բ�ι������ƶ������̶ȳߵ�һ�����������ʱ����һ������̱�Ե�������㴦�Ķ���ǡ���ǡ�2���͡�10������λ��cm������ô���̵�ֱ���ǣ������� ��ͼ���ڡ�ABC�У�CE��BF�������ߣ�����A=70�㣬��BCE=30�㣬���EBF���FBC�Ķ�����
��ͼ���ڡ�ABC�У�CE��BF�������ߣ�����A=70�㣬��BCE=30�㣬���EBF���FBC�Ķ�����