题目内容
4.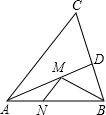 如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.
如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.
分析 根据AD是∠BAC的平分线确定出点B关于AD的对称点B′在AC上,根据垂线段最短,过点B′作B′N⊥AB于N交AD于M,根据轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,过点B作BE⊥AC于E,利用三角形的面积求出BE,再根据等腰三角形两腰上的高相等可得B′N=BE,从而得解.
解答 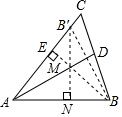 解:如图,∵AD是∠BAC的平分线,
解:如图,∵AD是∠BAC的平分线,
∴点B关于AD的对称点B′在AC上,
过点B′作B′N⊥AB于N交AD于M,
由轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,
过点B作BE⊥AC于E,
∵AC=10,S△ABC=25,
∴$\frac{1}{2}$×10•BE=25,
解得BE=5,
∵AD是∠BAC的平分线,B′与B关于AD对称,
∴AB=AB′,
∴△ABB′是等腰三角形,
∴B′N=BE=5,
即BM+MN的最小值是5.
故答案为:5.
点评 本题考查了轴对称确定最短路线问题,垂线段最短的性质,等腰三角形两腰上的高相等的性质,熟练掌握各性质并准确确定出点M的位置是解题的关键.

练习册系列答案
相关题目
19.-23的意义是( )
| A. | 3个-2相乘 | B. | 3个-2相加 | ||
| C. | -2乘以3 | D. | 3个2相乘的积的相反数 |
14.下列说法正确的是( )
| A. | 三点确定一个圆 | |
| B. | 经过圆心的直线是圆的对称轴 | |
| C. | 和半径垂直的直线是圆的切线 | |
| D. | 三角形的内心到三角形三个顶点距离相等 |