题目内容
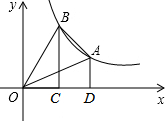 在反比例函数y=
在反比例函数y=| 8 |
| x |
(1)求点A、B的坐标;
(2)若AD⊥x轴,BC⊥x轴,垂足分别为点D、C,求S△AOB和S梯形ABCD.
考点:反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:计算题
分析:(1)先确定E的坐标为(1,2),从而得到点A的纵坐标为2,点B的横坐标为2,然后根据反比例函数图象上点的坐标特征求A点与B点坐标;
(2)由于S四边形ABOD=S△AOB+S△AOD=S△BOC+S梯形ABCD,根据反比例函数的比例系数k的几何意义得到S△BOC=S△AOD,所以S△AOB=S梯形ABCD,然后根据梯形的面积公式求解.
(2)由于S四边形ABOD=S△AOB+S△AOD=S△BOC+S梯形ABCD,根据反比例函数的比例系数k的几何意义得到S△BOC=S△AOD,所以S△AOB=S梯形ABCD,然后根据梯形的面积公式求解.
解答:解:(1)∵直线y=2x与直线x=1的交点E的坐标为(1,2),
∴点A的纵坐标为2,点B的横坐标为2,
当y=2时,
=2,解的x=4,A点坐标为(4,2),
当x=2时,y=
=4,则,B坐标为(2,4);
(2)∵S△BOC=S△AOD=
|8|=4,
而S四边形ABOD=S△AOB+S△AOD=S△BOC+S梯形ABCD,
∴S△AOB=S梯形ABCD=
(2+4)•(4-2)=6.
∴点A的纵坐标为2,点B的横坐标为2,
当y=2时,
| 8 |
| x |
当x=2时,y=
| 8 |
| x |
(2)∵S△BOC=S△AOD=
| 1 |
| 2 |
而S四边形ABOD=S△AOB+S△AOD=S△BOC+S梯形ABCD,
∴S△AOB=S梯形ABCD=
| 1 |
| 2 |
点评:本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
| k |
| x |

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,AB、CD为⊙O的直径,
如图,AB、CD为⊙O的直径,
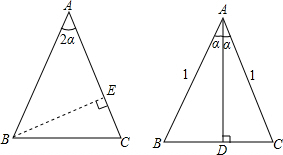 如图,在△ABC中,AB=AC=1,∠BAC=2α.请根据图中的提示,利用面积方法证明:sin2α=2sinα•cosα.
如图,在△ABC中,AB=AC=1,∠BAC=2α.请根据图中的提示,利用面积方法证明:sin2α=2sinα•cosα. 观察如图,用“>”或“<”填空.
观察如图,用“>”或“<”填空. 如图,AB=BD,AE=EB,∠ACB=∠ABC,证明:CD=2CE.
如图,AB=BD,AE=EB,∠ACB=∠ABC,证明:CD=2CE.