题目内容
6.在一条直线上依次有A、B、C三个港口,A、B两港相距30千米,B、C两港相距90千米.甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.甲0.5小时到达B港,此时两船相距15千米.求:(1)甲船何时追上乙,此时乙离C港多远?
(2)何时甲乙两船相距10千米.
分析 (1)先根据题意求得甲、乙两船的速度,然后根据甲船的路程比乙船的路程多30千米列方程求解即可;
(2)分为甲在乙的后面和甲在乙的前面两种情况列方程求解即可.
解答 解:(1)∵甲0.5小时到达B港,此时两船相距15千米,A、B两港相距30千米,
∴甲船的速度为60千米/小时,乙的速度为30千米/小时.
设x小时,甲追上乙.
根据题意得:60x=30x+30,
解得:x=1.
90-30×1=60千米.
答:两船出发1小时后甲船追上乙船,此时乙距离C港60千米.
(2)设x小时,甲乙两船相距10千米.
当甲在前乙在后时,60x=30+30x+10,
解得:x=$\frac{4}{3}$.
当甲在后乙在前时,60x=30+30x-10.
解得:x=$\frac{2}{3}$.
答:当甲乙两船出发$\frac{2}{3}$小时或$\frac{4}{3}$小时后两船相距10千米.
点评 本题主要考查的是一元一次方程的应用,找出题目的相等关系是解题的关键.

练习册系列答案
相关题目
 用一个平面去截一个三棱柱,截面可能是什么形状?先想一想,再做一做.
用一个平面去截一个三棱柱,截面可能是什么形状?先想一想,再做一做. 根据下面给出的数轴,解答下列问题:
根据下面给出的数轴,解答下列问题: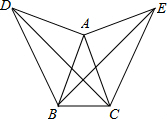 如图所示,在△ABC中,AB=AC,分别以AB,AC为直角边向外作两个等腰直角三角形△ABD和△ACE,使∠BAD=∠CAE=90°,求证:BE=CD.
如图所示,在△ABC中,AB=AC,分别以AB,AC为直角边向外作两个等腰直角三角形△ABD和△ACE,使∠BAD=∠CAE=90°,求证:BE=CD. 如图,点A、B坐标分别为(4,2)、(3,0),
如图,点A、B坐标分别为(4,2)、(3,0), 已知:如图,在等边△ABC中,D为边BC上一点,E是△ABC外一点,且CE∥AB,∠ADE=60°,求证:CE+CD=AB.
已知:如图,在等边△ABC中,D为边BC上一点,E是△ABC外一点,且CE∥AB,∠ADE=60°,求证:CE+CD=AB.