题目内容
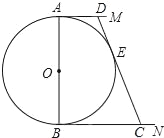
【题目】如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.
(1)若∠ADC=122°,求∠BCD的度数;
(2)设AD=x,BC=y,求y关于x的函数解析式.
【答案】(1)58°;(2)y=![]()
【解析】
(I)由于AD与BC都是⊙O的切线,易证AD∥BC,所以∠ADC+∠BCD=180°,从而可求出∠BCD的度数;
(II)过点D作DF⊥BC于点F,可知AB=CD=12,由切线长定理以及勾股定理即可求出x与y之间的关系式.
(1)∵AD与BC都是⊙O的切线,
∴∠OAD=∠OBC=90°,
∴∠OAD+∠OBC=180°,
∴AD∥BC,
∴∠BCD+∠ADC=180°,
∴∠BCD=58°;
(2)过点D作DF⊥BC于点F,

可知AB=CD=12,
∵AM和BN是⊙O的两条切线,DE与⊙O相切于点E,
∴AD=DE=x,BC=CE=y,
∴CD=DE+CE=x+y,
∴CF=BC﹣BF=y﹣x,
在Rt△DFC中,
∴由勾股定理可知:DF2+FC2=CD2,
122+(y﹣x)2=(x+y)2
∴化简可得:y=![]()

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
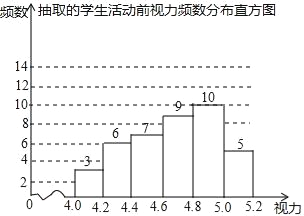
【题目】为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 3 |
4.4≤x<4.6 | 5 |
4.6≤x<4.8 | 8 |
4.8≤x<5.0 | 17 |
5.0≤x<5.2 | 5 |
(1)求活动所抽取的学生人数;
(2)若视力达到4.8及以上为达标,计算活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度评价视力保健活动的效果.