题目内容
9.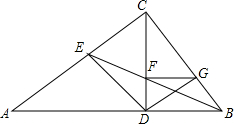 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ABC平分线交边AC于点E,交CD于F,过点F作FG∥AB,交边BC于点G,连结ED,GD.求证:$\frac{CE}{CD}$=$\frac{BG}{BD}$.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ABC平分线交边AC于点E,交CD于F,过点F作FG∥AB,交边BC于点G,连结ED,GD.求证:$\frac{CE}{CD}$=$\frac{BG}{BD}$.
分析 根据FG∥AB,得到△CFG∽△CDB,推出$\frac{CF}{CD}=\frac{FG}{BD}$,由平行线的性质得到∠BFG=∠FBD,由角平分线的定义得到∠FBG=∠FBD,于是得到△GFB是等腰三角形,FG=BG,由已知条件得到∠CFG=90°,求得∠CFE=180°-∠CFG-∠BFG=90°-∠FBG,证得∠CEB=∠CFE,得到CE=CF,等量代换即可得到结论.
解答 证明:∵FG∥AB,
∴△CFG∽△CDB,
∴$\frac{CF}{CD}=\frac{FG}{BD}$,
∵FG∥AB,
∴∠BFG=∠FBD,
∵BF是∠ABC的平分线,
∴∠FBG=∠FBD,
∴∠FBG=∠BFG,
∴△GFB是等腰三角形,FG=BG,
∵AB⊥CD,FG∥AB,
∴∠CFG=90°,
∴∠CFE=180°-∠CFG-∠BFG=90°-∠FBG,
在△ABE中,∠BCE=90°,
∴∠CEB=180°-∠BCE-∠EBC=90°-∠EBC,
∴∠CEB=∠CFE,
∴CE=CF,
∴$\frac{CE}{CD}$=$\frac{BG}{BD}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,三角形的内角和,角平分线的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
4.从正方形铁片,截去2cm宽的一条长方形,余下的矩形的面积是48cm2,则原来的正方形铁片的面积是( )
| A. | 8cm | B. | 64cm | C. | 8cm2 | D. | 64cm2 |
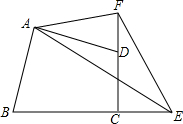 已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.
已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.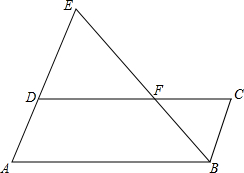 如图,F是?ABCD的边CD上一点,连接B对延长交AD的延长线于E.求证:$\frac{ED}{DA}=\frac{DF}{FC}$.
如图,F是?ABCD的边CD上一点,连接B对延长交AD的延长线于E.求证:$\frac{ED}{DA}=\frac{DF}{FC}$. B.
B.  C.
C.  D.
D. 