题目内容
20．
如图，点O是△ABC的重心，则$\frac{OB}{OD}$=2．
分析 根据重心的性质可求得BO：OD=2：1，即可求得．
解答 解：∵O为△ABC的重心，
∴BO：OD=2：1，
∴$\frac{OB}{OD}$=2．
故答案为：2．
点评 此题考查了三角形的重心，其性质：三角形的重心到顶点的距离是它到对边中点的距离的2倍．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．
如图，已知∠AOB，求作射线OC，使OC平分∠AOB．
①作射线OC．
②在OA和OB上分别截取OD、OE，使OD=OE．
③分别以D、E为圆心，以大于二分之一DE长为半径，在∠AOB内作弧，两弧交于点C．
作法合理的顺序是（ ）
如图，已知∠AOB，求作射线OC，使OC平分∠AOB．①作射线OC．
②在OA和OB上分别截取OD、OE，使OD=OE．
③分别以D、E为圆心，以大于二分之一DE长为半径，在∠AOB内作弧，两弧交于点C．
作法合理的顺序是（ ）
| A． | ①②③ | B． | ②①③ | C． | ③②① | D． | ②③① |
11．某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检，发现其中有5件不合格，那么你估计该厂这20万件产品中不合格品约为（ ）
| A． | 1万件 | B． | 2万件 | C． | 19万件 | D． | 20万件 |
8．下列各点在一次函数y=x+4图象上的是（ ）
| A． | 点（-7，3） | B． | 点（3，7） | C． | 点（4，-8） | D． | 点（2.5，1.5） |
5．
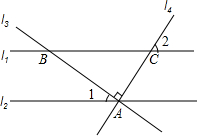如图，已知直线l1∥l2，直线l3⊥l4于A，在l2上，若∠1=27°，则∠2的度数为（ ）
如图，已知直线l1∥l2，直线l3⊥l4于A，在l2上，若∠1=27°，则∠2的度数为（ ）| A． | 27° | B． | 53° | C． | 63° | D． | 54° |
9．三条笔直的公路两两相交，若要建一座仓库，使它到三条公路的距离相等，则可供选择的点有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
10．
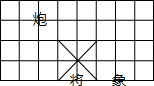若在象棋盘上建立直角坐标系，使“将”位于点（1，-1），“象”位于点（3，-1），则“炮”位于点（ ）
若在象棋盘上建立直角坐标系，使“将”位于点（1，-1），“象”位于点（3，-1），则“炮”位于点（ ）| A． | （1，3） | B． | （-1，1） | C． | （-1，2） | D． | （-1，3） |