Question

8．如图①A、E、F、C在一条直线上，AE=CF，过E、F分别作DE⊥AC，B F⊥AC，若AB=CD．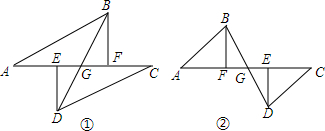
（1）图①中有3对全等三角形，并把它们写出来．
（2）求证：G是BD的中点．
（3）若将△ABF的边AF沿GA方向移动变为图②时，其余条件不变，第（2）题中的结论是否成立？如果成立，请予证明．

Answer 1

分析 （1）根据全等三角形的判定定理即可直接写出；
（2）首先证明△ABF≌△CDE，得到BF=DG，然后证明△DEG≌△BFG即可证得；
（3）与（2）证明方法相同．

解答 解：（1）图①中全等三角形有：△ABF≌△CDE，△ABG≌△CDG，△BFG≌△DEG．
故答案是：3；
（2）∵AE=CF，
∴AF=CE，
∴在直角△ABF和直角△CDE中，$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$，
∴△ABF≌△CDE，
∴BF=DE，
在△DEG和△BFG中，$\left\{\begin{array}{l}{∠GED=∠GFB}\\{∠DGE=∠BGF}\\{DE=BF}\end{array}\right.$，
∴△DEG≌△BFG，
∴BG=DG，即G是BD的中点；
（3）结论仍成立．
理由是：）∵AE=CF，
∴AF=CE，
在直角△ABF和直角△CDE中，$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$，
∴△ABF≌△CDE，
∴BF=DE，
在△DEG和△BFG中，$\left\{\begin{array}{l}{∠GED=∠GFB}\\{∠DGE=∠BGF}\\{DE=BF}\end{array}\right.$，
∴△DEG≌△BFG，
∴BG=DG，即G是BD的中点．

点评 本题考查了全等三角新的判定与性质，证明BF=DE是解决本题的关键．