题目内容
6.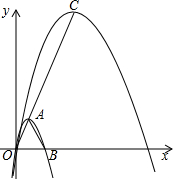 如图,抛物线C1:y=-$\sqrt{3}$x2+2$\sqrt{3}$x的顶点为A,与x轴的正半轴交于点B.
如图,抛物线C1:y=-$\sqrt{3}$x2+2$\sqrt{3}$x的顶点为A,与x轴的正半轴交于点B.(1)将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
(2)将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2,抛物线C2的顶点为C,点P在抛物线C2上,满足S△PAC=S△ABC,且∠ACP=90°.
①当k>1时,求k的值;
②当k<-1时,请直接写出k的值,不必说明理由.
分析 (1)由抛物线C1解析式求出A、B及原点坐标,将三点坐标都扩大到原来的2倍,待定系数求解可得;
(2)①如图1中,当k>1时,与(1)同理可得抛物线C2的解析式为y=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x及顶点C的坐标,根据S△PAC=S△ABC知BP∥AC,继而可得△ABO是边长为2的正三角形,四边形CEBP是矩形,表示出点P的坐标,将其代入到抛物线C2解析式可求得k的值;
②如图2中,当k<-1时,作△ABO关于y轴对称的△A′B′O,OE′⊥A′B′,同理可得四边形CEBP是矩形,先求出抛物线C2解析式,表示出点P的坐标,将其代入到抛物线C2解析式可求得k的值;
解答 解:(1)∵y=-$\sqrt{3}$x2+2$\sqrt{3}$x=-$\sqrt{3}$(x-1)2+$\sqrt{3}$,
∴抛物线C1经过原点O,点A(1,$\sqrt{3}$)和点B(2,0)三点,
∴变换后的抛物线经过原点O,(2,2$\sqrt{3}$)和(4,0)三点,
∴变换后抛物线的解析式为y=-$\frac{\sqrt{3}}{2}$x2+2$\sqrt{3}$x;
(2)①如图1中,当k>1时,
∵抛物线C2经过原点O,(k,$\sqrt{3}$k),(2k,0)三点,
∴抛物线C2的解析式为y=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x,
∴O、A、C三点共线,且顶点C为(k,$\sqrt{3}$k),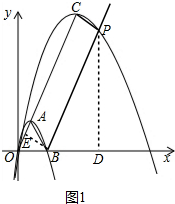
如图,∵S△PAC=S△ABC,
∴BP∥AC,
过点P作PD⊥x轴于D,过点B作BE⊥AO于E,
由题意知△ABO是边长为2的正三角形,四边形CEBP是矩形,
∴OE=1,CE=BP=2k-1,
∵∠PBD=60°,
∴BD=k-$\frac{1}{2}$,PD=$\frac{\sqrt{3}}{2}$(2k-1),
∴P(k+$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$(2k-1)),
∴$\frac{\sqrt{3}}{2}$(2k-1)=-$\frac{\sqrt{3}}{k}$(k+$\frac{3}{2}$)2+2$\sqrt{3}$(k+$\frac{3}{2}$),
解得:k=$\frac{9}{2}$;
②如图2中,当k<-1时,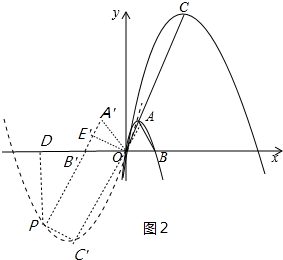
∵抛物线C2经过原点O,(k,$\sqrt{3}$k),(2k,0)三点,
∴抛物线C2的解析式为y=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x,
∴O、A、C′三点共线,且顶点C′为(k,$\sqrt{3}$k),
作△ABO关于y轴对称的△A′B′O,OE′⊥A′B′,
∵S△PAC′=S△ABC=S△AC′B′,
∴A′P∥AC′,由题意四边形PC′OE′是矩形,
∴PE′=OC′=-2k,B′E′=1,PB′=-2k-1,
在Rt△PDB′中,∵∠PDB′=90°,∠PB′D=∠A′B′O=60°,
∴DB′=$\frac{1}{2}$PB′=$\frac{-2k-1}{2}$,DP=$\frac{\sqrt{3}}{2}$(-2k-1),
∴点P坐标[$\frac{2k-3}{2}$,$\frac{\sqrt{3}}{2}$(2k+1)],
∴$\frac{\sqrt{3}}{2}$(2k+1)=-$\frac{\sqrt{3}}{k}$($\frac{2k-3}{2}$)2+2$\sqrt{3}$($\frac{2k-3}{2}$)
∴k=-$\frac{9}{2}$.
点评 本题主要考查待定系数求函数解析式及二次函数的性质、解直角三角形等知识点,根据题意表示出点P的坐标是解题的关键,学会添加辅助线构造特殊四边形解决问题,属于中考压轴题.

| x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(2)$\sqrt{28561}$≈169.
(3)$\sqrt{273}$在那两个相邻数之间?为什么?
| A. | 2a2-a2=1 | B. | (a+b)2=a2+b2 | C. | (3b3)2=6b6 | D. | (-a)5÷(-a)3=a2 |