题目内容
19.估计$\sqrt{5}$+1的值在( )| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
分析 利用”夹逼法“得出$\sqrt{5}$的范围,继而也可得出$\sqrt{5}$+1的范围.
解答 解:∵2=$\sqrt{4}$<$\sqrt{5}$<$\sqrt{9}$=3,
∴3<$\sqrt{5}$+1<4,
故选B.
点评 此题考查了估算无理数的大小的知识,属于基础题,解答本题的关键是掌握夹逼法的运用.

练习册系列答案
相关题目
9.下列等式正确的有( )
①a4b2=(ab)6; ②(10n+1)2=102n+2;③25+25=210; ④${({x^n})^n}•{x^n}={x^{{n^2}+n}}$.
①a4b2=(ab)6; ②(10n+1)2=102n+2;③25+25=210; ④${({x^n})^n}•{x^n}={x^{{n^2}+n}}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列各式正确的是( )
| A. | $\sqrt{{{(-5)}^2}}=-5$ | B. | $-\sqrt{{{(-15)}^2}}=-15$ | C. | $\sqrt{{{(-5)}^2}}=±5$ | D. | $\sqrt{\frac{1}{2}}=\frac{1}{2}$ |
11.已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3等于( )
| A. | 150° | B. | 180° | C. | 210° | D. | 120° |
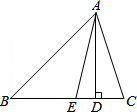 如图△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠DAE=14°,求∠BAE和∠C的度数.
如图△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠DAE=14°,求∠BAE和∠C的度数.