题目内容
 二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是( )| A、ac>0 |
| B、b<0 |
| C、2a+b=0 |
| D、b2-4ac<0 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:A、由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上,
可得c>0,因此ac<0,故不正确;
B、对称轴为x=-
=1,得2a=-b,可得a、b异号,即b>0,故错误;
C、对称轴为x=-
=1,得2a=-b,即2a+b=0,故正确,
D、而抛物线与x轴有两个交点,可得b2-4ac>0,故错误.
故选:C.
可得c>0,因此ac<0,故不正确;
B、对称轴为x=-
| b |
| 2a |
C、对称轴为x=-
| b |
| 2a |
D、而抛物线与x轴有两个交点,可得b2-4ac>0,故错误.
故选:C.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套?( )
| A、16、20 |
| B、18、18 |
| C、12、24 |
| D、20、16 |
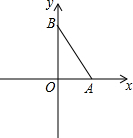 如图,在平面直角坐标系中,点A,B分别在x轴,y轴上,且∠ABO=30°,点P在坐标轴上且使△ABP为等腰三角形,则满足条件的点P共有
如图,在平面直角坐标系中,点A,B分别在x轴,y轴上,且∠ABO=30°,点P在坐标轴上且使△ABP为等腰三角形,则满足条件的点P共有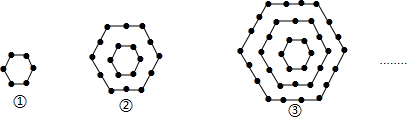
 如图,在半径为10cm的⊙O中作一个正六边形ABCDEF,(要求尺规作图)并试求此正六边形的面积.
如图,在半径为10cm的⊙O中作一个正六边形ABCDEF,(要求尺规作图)并试求此正六边形的面积.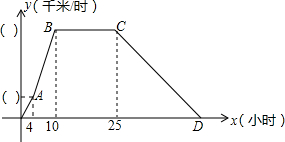 某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒地,风速变为平均每小时增加4千米/时,一段时间,风暴保持变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止.结合风速与时间的图象,回答下列问题:
某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒地,风速变为平均每小时增加4千米/时,一段时间,风暴保持变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止.结合风速与时间的图象,回答下列问题: