题目内容
16.把分式$\frac{1}{x-y}$,$\frac{1}{x+y}$,$\frac{1}{{x}^{2}-{y}^{2}}$进行通分,它们的最简公分母是( )| A. | x-y | B. | x+y | C. | x2-y2 | D. | (x+y)(x-y)(x2-y2) |
分析 确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
解答 解:分式$\frac{1}{x-y}$,$\frac{1}{x+y}$,$\frac{1}{{x}^{2}-{y}^{2}}$的分母分别是(x-y)、(x+y)、(x+y)(x-y).
则最简公分母是(x+y)(x-y)=x2-y2.
故选:C.
点评 本题考查了最简公分母的定义及确定方法,通分的关键是准确求出各个分式中分母的最简公分母,确定最简公分母的方法一定要掌握.

练习册系列答案
相关题目
6.下列调查中,调查方式选择合理的是( )
| A. | 为了了解全国中学生的视力情况,选择全面调查 | |
| B. | 为了了解一批袋装食品是否含有防腐剂,选择全面调查 | |
| C. | 为了检测某城市的空气质量,选择抽样调查 | |
| D. | 为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查 |
8.已知直线y=x+1,那么该直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.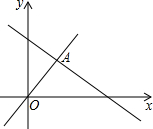 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为( )| A. | x$≤\frac{3}{2}$ | B. | x≥3 | C. | x$≥\frac{3}{2}$ | D. | x≤3 |