题目内容
17. 如图,AB∥CD,CD为⊙O的直径,⊙O的半径等于3,∠ACB=30°,求图中阴影部分的面积.
如图,AB∥CD,CD为⊙O的直径,⊙O的半径等于3,∠ACB=30°,求图中阴影部分的面积.
分析 如图,连接OA.S阴影=S半圆-S扇形OAD-S△AOC.
解答 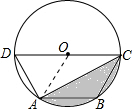 解:如图,连接OA,
解:如图,连接OA,
∵∠ACB=30°,
∴∠AOD=60°.
∴∠AOC=120°,
∴S阴影=S半圆-S扇形OAD-S△AOC,
=$\frac{1}{2}$×32π-$\frac{60π×{3}^{2}}{360}$-$\frac{1}{2}$×3×3×sin120°=3π-$\frac{9\sqrt{3}}{4}$.即图中阴影部分的面积是3π-$\frac{9\sqrt{3}}{4}$.
点评 此题考查了扇形的面积公式,求阴影部分的面积时,利用了“分割法”.

练习册系列答案
相关题目
8.有一列数a1、a2、a3、…an,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a1=-1,则a2013=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 2012 |
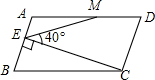 如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°.
如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°.
 如图,在矩形ABCD中,AB=10,BC=8,E为AD边上的一点,沿CE将△CDE对折,使点D正好落在AB边上,记落点为F,求sin∠AFE的值.
如图,在矩形ABCD中,AB=10,BC=8,E为AD边上的一点,沿CE将△CDE对折,使点D正好落在AB边上,记落点为F,求sin∠AFE的值. 如图,已知AB与CD交于点O,且△AOC≌△BOD,求证:AC∥BD.
如图,已知AB与CD交于点O,且△AOC≌△BOD,求证:AC∥BD.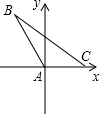 如图,AB=6,AC=5,∠BAC=120°.求(1)B点的坐标;(2)BC的长.
如图,AB=6,AC=5,∠BAC=120°.求(1)B点的坐标;(2)BC的长.