Question

9．如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连接OB、OC，若∠BOC与∠BAC互补，则弦BC的长为2$\sqrt{3}$．

Answer 1

分析 首先过点O作OD⊥BC于D，由垂径定理可得BC=2BD，又由圆周角定理，可求得∠BOC的度数，然后根据等腰三角形的性质，求得∠OBC的度数，利用余弦函数，即可求得答案．

解答 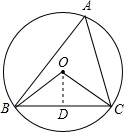解：过点O作OD⊥BC于D，
则BC=2BD，
∵△ABC内接于⊙O，∠BAC与∠BOC互补，
∴∠BOC=2∠A，∠BOC+∠A=180°，
∴∠BOC=120°，
∵OB=OC，
∴∠OBC=∠OCB=$\frac{1}{2}$（180°-∠BOC）=30°，
∵⊙O的半径为2，
∴BD=OB•cos∠OBC=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，
∴BC=2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．

点评 此题考查了圆周角定理、垂径定理、等腰三角形的性质以及三角函数等知识．注意掌握辅助线的作法，注意数形结合思想的应用．