题目内容
11. 如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是⊙O的切线.
(2)若PB=3,DB=4,求DE的长.
分析 (1)由已知角相等,及对顶角相等得到三角形DOE与三角形POB相似,利用相似三角形对应角相等得到∠OBP为直角,即可得证;
(2)在直角三角形PBD中,由PB与DB的长,利用勾股定理求出PD的长,由切线长定理得到PC=PB,由PD-PC求出CD的长,在直角三角形OCD中,设OC=r,则有OD=8-r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,然后通过相似三角形的性质即可得到结论.
解答 (1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线;
(2)解:在Rt△PBD中,PB=3,DB=4,
根据勾股定理得:PD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵PD与PB都为圆的切线,
∴PC=PB=3,
∴DC=PD-PC=5-3=2,
在Rt△CDO中,设OC=r,则有DO=4-r,
根据勾股定理得:(4-r)2=r2+22,
解得:r=$\frac{3}{2}$,
∴OP=$\sqrt{P{C}^{2}+O{C}^{2}}$=$\frac{3\sqrt{5}}{2}$,
∵∠E=∠PBO,∠DPE=∠OPB,
∴△DEP∽△OBP,
∴$\frac{DE}{OB}=\frac{DP}{OP}$,
∴DE=$\sqrt{5}$.
点评 此题考查了切线的判定与性质,勾股定理,相似三角形的判定和性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.长城、故宫等是我国第一批成功入选世界遗产的文化古迹,长城总长约6700 000米.将6700 000用科学记数法表示应为( )
| A. | 67×106 | B. | 6.7×106 | C. | 6.7×106 | D. | 0.67×106 |
1. 实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是( )
 实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是( )| A. | a和d | B. | a和c | C. | b和d | D. | b和c |
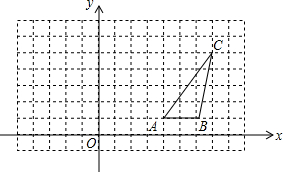 如图,△ABC的顶点坐标分别为(4,1),B(6,1),C(7,5)
如图,△ABC的顶点坐标分别为(4,1),B(6,1),C(7,5)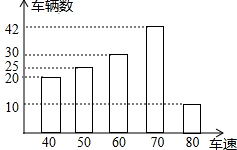 为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是70千米/时.
为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是70千米/时.