题目内容
13.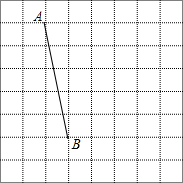 如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.
如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.(Ⅰ)AB的长等于$\sqrt{26}$;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,在线段AB上画出点P,使AP=$\frac{5\sqrt{26}}{7}$,并简要说明画图方法(不要求证明).
分析 (Ⅰ)利用格点,根据勾股定理求出AB的长;
(Ⅱ)根据三角形相似,使得AP为AB长度的$\frac{5}{7}$即可.
解答  解:(Ⅰ)AB=$\sqrt{{1}^{2}+{5}^{2}}$=$\sqrt{26}$;
解:(Ⅰ)AB=$\sqrt{{1}^{2}+{5}^{2}}$=$\sqrt{26}$;
(Ⅱ)取格点C、D,连接CD,CD与AB交于点P,则点P即为所求.(可根据△APC∽△BPD证明)
故答案为$\sqrt{26}$.
点评 本题考查了勾股定理,充分利用格点的特点和相似三角形的性质是解题的关键.

练习册系列答案
相关题目
1.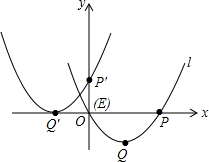 如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
 如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )| A. | (-1,$\frac{1}{2}$) | B. | (0,0) | C. | (-$\frac{1}{2}$,1) | D. | (-$\frac{1}{2}$,0) |
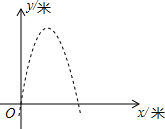 滕州市政府大楼前广场有一喷水池,喷出水的路径是一条抛物线,如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空号总划出的曲线是抛物线y=-x2+6x(单位:米)的一部分,则水喷出的最大高度是9米.
滕州市政府大楼前广场有一喷水池,喷出水的路径是一条抛物线,如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空号总划出的曲线是抛物线y=-x2+6x(单位:米)的一部分,则水喷出的最大高度是9米.