题目内容
18．某商店经营一种成本为每千克40美元的水产品，根据市场分析，若按每千克50元销售，一个月能售出500千克；销售价每涨1元，月销售量就减少10千克，（1）针对这种水产品的销售情况，设销售单价定为x元（x＞50），请用的x代数式表示月销售量，以及获得的利润．
（2）当x取什么数时利润最大？最大利润是多少？
分析 （1）月销售利润=每千克的利润×可卖出千克数，把相关数值代入即可；
（2）利用公式法可得二次函数的最值．
解答 解：（1）可卖出千克数为500-10（x-50）=1000-10x，
y与x的函数表达式为y=（x-40）（1000-10x）=-10x2+1400x-40000，
（2）∵y=-10x2+1400x-40000=-10（x-70）2+9000
∴当x=70时，y有最大值9000．
答：商店销售单价应定为70元时，销售利润最大，为9000元．
点评 考查二次函数的应用；得到可卖出千克数是解决本题的难点，解题的关键点时从实际问题中抽象出二次函数模型，难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．下列分数中，能化为有限小数的是（ ）
| A． | $\frac{1}{15}$ | B． | $\frac{2}{15}$ | C． | $\frac{3}{15}$ | D． | $\frac{5}{15}$ |
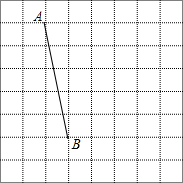如图，将线段AB放在每个小正方形的边长为1的网格中，点A，点B均落在格点上．
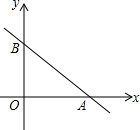在平面直角坐标系中，一次函数y=-$\frac{3}{4}$x+3的图象与x、y轴分别交于点A、B．
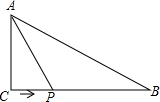如图，在Rt△ABC中，已知∠C=90°，边AC=4cm，BC=5cm，点P为CB边上一点，当动点P沿CB从点C向点B运动时，△APC的面积发生了变化．