题目内容
△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于BC的中点处.
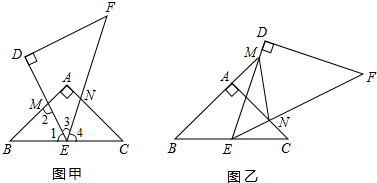
①如图甲,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
②如图乙,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N.求证:△ECN∽△MEN.
①如图甲,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
②如图乙,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N.求证:△ECN∽△MEN.

考点:相似三角形的判定
专题:
分析:(1)由△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,易得∠2=∠4,又由∠B=∠C=45°,即可证得△BEM∽△CNE;
(2)与(1)同理△BEM∽△CNE,可得
=
,又由BE=EC,即可得
=
,然后由∠ECN=∠MEN=45°,证得△ECN∽△MEN.
(2)与(1)同理△BEM∽△CNE,可得
| BE |
| CN |
| EM |
| NE |
| EC |
| CN |
| EM |
| NE |
解答:证明:(1)∵△ABC是等腰直角三角形,
∴∠B=45°,
∴∠1+∠2=135°
又∵△DEF是等腰直角三角形,
∴∠3=45°
∴∠1+∠4=135°
∴∠2=∠4,
∵∠B=∠C=45°,
∴△BEM∽△CNE;
(2)与(1)同理△BEM∽△CNE,
∴
=
,
又∵BE=EC,
∴
=
,
∴
=
,
又∵∠ECN=∠MEN=45°,
∴△ECN∽△MEN.
∴∠B=45°,
∴∠1+∠2=135°
又∵△DEF是等腰直角三角形,
∴∠3=45°
∴∠1+∠4=135°
∴∠2=∠4,
∵∠B=∠C=45°,
∴△BEM∽△CNE;
(2)与(1)同理△BEM∽△CNE,
∴
| BE |
| CN |
| EM |
| NE |
又∵BE=EC,
∴
| EC |
| CN |
| EM |
| NE |
∴
| EC |
| EM |
| CN |
| NE |
又∵∠ECN=∠MEN=45°,
∴△ECN∽△MEN.
点评:此题考查了相似三角形的判定与性质以及等腰直角三角形性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若x、y互为不等于0的相反数,且n是正整数,你认为正确的是( )
| A、xn、yn一定互为相反数 | ||||
B、(
| ||||
| C、x2n、y2n一定互为相反数 | ||||
| D、x2n-1、-y2n-1一定相等 |
 如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D,若AD=12,TC=8,则⊙O半径为
如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D,若AD=12,TC=8,则⊙O半径为 如图,用长6m的铝合金条制成“日“字形窗框,请问宽和高各是多少时,窗户的透光面积为1.5m2(铝合金条的宽度不计)?
如图,用长6m的铝合金条制成“日“字形窗框,请问宽和高各是多少时,窗户的透光面积为1.5m2(铝合金条的宽度不计)? 如图,在四边形ABCD中,∠C+∠D=α°,∠A,∠B的平分线相交于点O,求∠O的度数.
如图,在四边形ABCD中,∠C+∠D=α°,∠A,∠B的平分线相交于点O,求∠O的度数.