题目内容
当m取何值时,
=
.
| x+m |
| 2x-3 |
| (x+m)(2m+2) |
| (2x-3)(m-2) |
考点:解分式方程
专题:
分析:分为两种情况:①当x+m=0,即x=-m时,根据分式有意义的条件得出x≠
,且m-2≠0,即可求出m的范围;②当x+m≠0,即x≠-m时,方程变形得:
=
,解方程,即可得出答案.
| 3 |
| 2 |
| 1 |
| 2x-3 |
| 2m+2 |
| (2x-3)(m-2) |
解答:解:①当x+m=0,即x=-m时,x≠
,且m-2≠0,
即m≠-
,m≠2;
②当x+m≠0,即x≠-m时,方程变形得:
=
,
去分母得:m-2=2m+2,
m=-4
综合上述:当m≠-
且m≠2或m=-4时,
=
.
| 3 |
| 2 |
即m≠-
| 3 |
| 2 |
②当x+m≠0,即x≠-m时,方程变形得:
| 1 |
| 2x-3 |
| 2m+2 |
| (2x-3)(m-2) |
去分母得:m-2=2m+2,
m=-4
综合上述:当m≠-
| 3 |
| 2 |
| x+m |
| 2x-3 |
| (x+m)(2m+2) |
| (2x-3)(m-2) |
点评:此题考查了解分式方程的应用,题目比较典型,但是有一定的难度,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
直线y=kx+b经过A(0.2)和B(3.0)两点,那么这个一次函数关系式是( )
| A、y=2x+3 | ||
B、y=-
| ||
| C、y=3x+2 | ||
| D、y=x+1 |
0.5的相反数是( )
| A、-0.5 | B、0.5 |
| C、2 | D、-2 |
点P(m+1,n)向下平移4个单位后,关于y轴对称的点的坐标为(-1,-5),则点P的坐标为( )
| A、(1,-1) |
| B、(1,1) |
| C、(-1,1) |
| D、(-1,-1) |
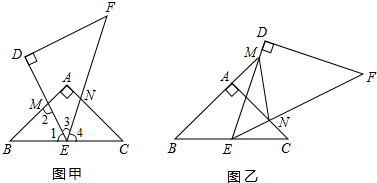
 已知,如图,BE平分∠ABC,DE∥BC,∠1=35°,求:
已知,如图,BE平分∠ABC,DE∥BC,∠1=35°,求: