Question

6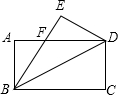．已知长方形ABCD中，AD=8，AB=4，将长方形沿着BD对折，点C的对应点是点E，AD与BE相交于点F．
（1）请说明△BFD是等腰三角形．
（2）请计算AF的长度．

Answer 1

分析 （1）由折叠的性质有∠FBD=∠CBD，由于AD∥BC得到∠FDB=∠DBC，于是有∠FDB=∠FBD，根据等腰三角形的判定即可证得结论；
（2）根据折叠的性质得到BE=BC=8，根据勾股定理即可得到结论．

解答 解：（1）∵将长方形沿着BD对折，点C的对应点是点E，
∴∠DBF=∠CBD，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠ADB=∠DBC，
∴∠FDB=∠FBD，
∴△BFD是等腰三角形；

（2）根据折叠可得BE=BC=8，
在Rt△ABF中，设AF=x，则BF=8-x，
x²+4²=（8-x）²，
解得：x=3，
即AF=3．

点评 本题考查的是翻折变换的性质、全等三角形的判定与性质、勾股定理，熟知图形翻折变换的性质是解答此题的关键．