题目内容
15．
抛物线y=ax2+bx+c与直线y=mx+n的图象如图：（1）方程ax2+bx+c=mx+n的解为-2，1．
（2）不等式ax2+bx+c＞mx+n的解集为x＞1或x＜-2．
分析 （1）直接利用两图象的交点横坐标即为方程ax2+bx+c=mx+n的解得出答案；
（2）利用函数图象得出不等式ax2+bx+c＞mx+n的解集．
解答 解：（1）如图所示：两图象的交点横坐标为：-2，1，
则方程ax2+bx+c=mx+n的解为：-2，1；
故答案为：-2，1；
（2）不等式ax2+bx+c＞mx+n的解集，即二次函数图象在一次函数图象上面x的取值范围：x＞1或x＜-2．
故答案为：x＞1或x＜-2．
点评 此题主要考查了二次函数与不等式以及二次函数与一元二次方程，正确利用数形结合得出是解题关键．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
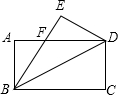已知长方形ABCD中，AD=8，AB=4，将长方形沿着BD对折，点C的对应点是点E，AD与BE相交于点F．