题目内容
16. 如图,AD为△ABC的中线,BE为△ABD中线.
如图,AD为△ABC的中线,BE为△ABD中线.(1)若∠ABE=15°,∠BAD=35°,求∠BED的度数.
(2)若△ABC的面积为36,BD=6,则点E到BC边的距离为多少?
分析 (1)根据三角形的外角性质进行计算即可;
(2)根据三角形的中线将三角形分成面积相等的两部分,求得△BDE的面积,再根据三角形的面积公式,求得点E到BC边的距离为3.
解答 解:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAE=15°+35°=50°;
(2)∵AD为△ABC的中线,BE为△ABD中线,
∴△ABC的面积=2×△ABD的面积,△ABD的面积=2×△BDE的面积,
∵△ABC的面积为36,BD=6,
∴△BDE的面积=9,
设点E到BC边的距离为x,则$\frac{1}{2}$×BD×x=9,
即$\frac{1}{2}$×6×x=9,
∴x=3
∴点E到BC边的距离为3.
点评 本题主要考查了三角形的面积计算,解决问题的关键是掌握:三角形的面积等于底边长与高线乘积的一半,即S△=$\frac{1}{2}$×底×高;三角形的中线将三角形分成面积相等的两部分.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
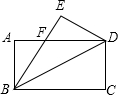 已知长方形ABCD中,AD=8,AB=4,将长方形沿着BD对折,点C的对应点是点E,AD与BE相交于点F.
已知长方形ABCD中,AD=8,AB=4,将长方形沿着BD对折,点C的对应点是点E,AD与BE相交于点F. 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2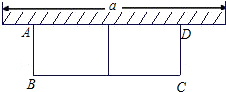 如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成中间隔有一道篱笆的长方形花圃.如果要围成面积为45平方米的花圃,AB的长是多少米?
如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成中间隔有一道篱笆的长方形花圃.如果要围成面积为45平方米的花圃,AB的长是多少米?