题目内容
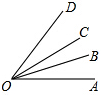
 如图,O为直线AB上一点,OE平分∠BOC,∠EOD=90°,∠COE=18°.
如图,O为直线AB上一点,OE平分∠BOC,∠EOD=90°,∠COE=18°.(1)求∠AOD的度数;
(2)OD平分∠AOC吗?请说明理由.
考点:角的计算,角平分线的定义
专题:
分析:(1)根据∠EOD=90°,∠COE=18°,可得出∠EOB+∠AOD=90°,再由OE平分∠BOC,得∠COE=∠BOE;
(2)由(1)再计算得出∠COD,再得结论.
(2)由(1)再计算得出∠COD,再得结论.
解答:解:(1)∵OE平分∠BOC,
∴∠COE=∠BOE,
∵∠COE=18°,
∴∠BOE=18°,
∵∠EOD=90°,
∴∠EOB+∠AOD=90°,
∴∠AOD=72°;
(2)OD平分∠AOC,
理由是:
∵∠EOD=90°,
∴∠EOC+∠COD=90°,
∵∠COE=18°,
∴∠COD=72°,
∵∠AOD=72°,
∴∠COD=∠AOD=72°,
∴OD平分∠AOC.
∴∠COE=∠BOE,
∵∠COE=18°,
∴∠BOE=18°,
∵∠EOD=90°,
∴∠EOB+∠AOD=90°,
∴∠AOD=72°;
(2)OD平分∠AOC,
理由是:
∵∠EOD=90°,
∴∠EOC+∠COD=90°,
∵∠COE=18°,
∴∠COD=72°,
∵∠AOD=72°,
∴∠COD=∠AOD=72°,
∴OD平分∠AOC.
点评:本题考查了角的计算和角平分线的定义,解题的关键是求一个角的余角.

练习册系列答案
相关题目
 看图填空:
看图填空: (1)已知a,b都是有理数,在数轴上的位置如图所示,则a,-b,|a|,|b|的大小关系是:
(1)已知a,b都是有理数,在数轴上的位置如图所示,则a,-b,|a|,|b|的大小关系是: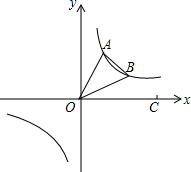 如图,点A(3,6),B(6,a)是反比例函数y=
如图,点A(3,6),B(6,a)是反比例函数y= 如图,在一个长为300米,宽为200米的长方形场地上修三条不同形状的小路,剩余部分作为绿化区种植花草.已知三条小路的边缘长都为x,让各条小路的两边分别平行.若绿化面积为53200平方米,求小路的边缘长x.
如图,在一个长为300米,宽为200米的长方形场地上修三条不同形状的小路,剩余部分作为绿化区种植花草.已知三条小路的边缘长都为x,让各条小路的两边分别平行.若绿化面积为53200平方米,求小路的边缘长x.