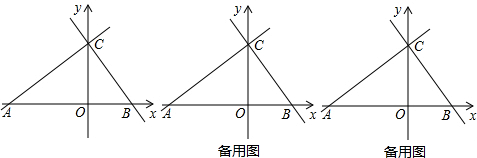
题目内容
 (1)画出图中△ABC的高AD(标注出点D的位置);画出图中△ABC的角平分线AE(标注出点E的位置);
(1)画出图中△ABC的高AD(标注出点D的位置);画出图中△ABC的角平分线AE(标注出点E的位置);(2)若∠C=n°,∠ABC=m°,求∠DAE的度数;
(3)若BE:EC=2:3,EF为△AEC的中线,△ABC的面积为1,则△CEF的面积为
考点:作图—复杂作图,三角形的面积
专题:计算题,作图题
分析:(1)根据三角形的高、角平分线定义画出图形;
(2)根据角平分线定义可得∠CAE=
∠CAB=
n°,然后表示出∠AEC,再根据内角与外角的性质可得∠DAE的度数;
(3)根据边长比可得S△AEC:S△ABE=2:3,再根据三角形的中线平分三角形的面积可得答案.
(2)根据角平分线定义可得∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据边长比可得S△AEC:S△ABE=2:3,再根据三角形的中线平分三角形的面积可得答案.
解答:解:(1)如图所示:
(2)∵AE平分∠CAB,
∴∠CAE=
∠CAB=
n°,
∵∠ABC=m°,
∴∠C=180°-m°-n°,
∴∠AEC=180°-
n°-(180°-m°-n°)=(m+
n)°,
∴∠EAD=(m+
n-90)°;
(3)∵BE:EC=2:3,
∴S△AEC:S△ABE=2:3,
∵△ABC的面积为1,
∴S△AEC=
,
∵EF为△AEC的中线,
∴△CEF的面积为:
×
=
.
(2)∵AE平分∠CAB,

∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=m°,
∴∠C=180°-m°-n°,
∴∠AEC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EAD=(m+
| 1 |
| 2 |
(3)∵BE:EC=2:3,
∴S△AEC:S△ABE=2:3,
∵△ABC的面积为1,
∴S△AEC=
| 3 |
| 5 |
∵EF为△AEC的中线,
∴△CEF的面积为:
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
点评:此题主要考查了复杂作图,以及三角形的内角和,关键是掌握角平分线和高线的画法.

练习册系列答案
相关题目
 a、b两个有理数在数轴上对应的点的位置如图,把a,-a,b,-b按照由大到小的顺序排列正确的是( )
a、b两个有理数在数轴上对应的点的位置如图,把a,-a,b,-b按照由大到小的顺序排列正确的是( )| A、b>-a>a>-b |
| B、b>a>-a>-b |
| C、b>a>-b>-a |
| D、a>-a>b>-b |
 画图解决问题
画图解决问题