题目内容
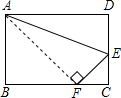如图，折叠矩形，使点D落在BC边上的点F处，BC=10cm，AB=8cm，则FC=考点：翻折变换（折叠问题）
专题：
分析：由图形翻折变换的性质可知，AD=AF，设BF=x，则FC=10-x，在Rt△ABF中利用勾股定理即可求解．
解答：解：∵△AEF是△AED沿直线AE折叠而成，AB=8cm，BC=10cm，
∴AD=AF=10cm，设BF=x，则FC=10-x，
在Rt△ABF中，AF2=AB2+BF2，即102=82+x2，
解得x=6，
∴FC=BC-BF=10-6=4cm．
故答案为：4cm．
∴AD=AF=10cm，设BF=x，则FC=10-x，
在Rt△ABF中，AF2=AB2+BF2，即102=82+x2，
解得x=6，
∴FC=BC-BF=10-6=4cm．
故答案为：4cm．
点评：本题考查的是图形翻折变换的性质，即折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
字词句段篇系列答案
相关题目
如图，在?ABCD中，点E、F分别在AD、BC上，且AE=CF．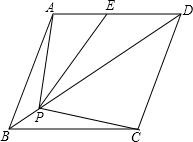
菱形ABCD的边长为2，∠ABC=60°，E是AD边中点，点P是对角线BD上的动点，当AP+PE的值最小时，PC的长是
如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示，则顶点A55的坐标是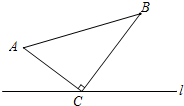
如图，△ABC中，∠ACB=90°，AC=7cm，BC=1lcm．点M从A点出发沿A→C→B路径向终点运动，终点为B点；点N从B点出发沿B→C→A路径向终点运动，终点为A点．点M和N分别以每秒1cm和3cm的运动速度同时开始运动，两点都要到达相应的终点时才能停止运动，分别过M和N作ME⊥l于E，NF⊥l于F．设运动时间为t秒，则当t=下列调查适合采用“普查”的是（ ）
| A、了解在校大学生的主要娱乐方式 |
| B、了解某个班级学生的体重 |
| C、一批灯泡的使用寿命 |
| D、调查《新闻联播》电视栏目的收视率 |