题目内容
17.化简:($\frac{x+3}{{x}^{2}+x-6}$-$\frac{x}{{x}^{2}-4}$)÷$\frac{1}{x+2}$,并求x=$\frac{1}{2-\sqrt{3}}$时的值.分析 根据分式的减法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:($\frac{x+3}{{x}^{2}+x-6}$-$\frac{x}{{x}^{2}-4}$)÷$\frac{1}{x+2}$
=$[\frac{x+3}{(x+3)(x-2)}-\frac{x}{(x+2)(x-2)}]•(x+2)$
=$[\frac{1}{x-2}-\frac{x}{(x+2)(x-2)}]•(x+2)$
=$\frac{x+2-x}{(x+2)(x-2)}•(x+2)$
=$\frac{2}{x-2}$,
当x=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$时,原式=$\frac{2}{2+\sqrt{3}-2}=\frac{2\sqrt{3}}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
16.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=$\frac{9}{2}$;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.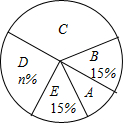 某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
根据以上信息,解答下列问题:
(1)被调查的学生中,每天参加体育锻炼的时间不少于90min的有18人,这些学生数占被调查总人数的百分比为15%,每天参加体育锻炼的时间不足60min的有30人;
(2)被调查的学生总数为120人,统计表中m的值为42,统计图中n的值为25,被调查学生每天参加体育锻炼时间的中位数落在C组;
(3)该校共有960名学生,根据调查结果,估计该校每天参加体育锻炼的时间不少于60min的学生数.
 某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.| 组别 | A | B | C | D | E |
| 时间t/min | t<45 | 45≤t<60 | 60≤t<75 | 75≤t<90 | t≥90 |
| 人数 | 12 | 18 | m | 30 | 18 |
(1)被调查的学生中,每天参加体育锻炼的时间不少于90min的有18人,这些学生数占被调查总人数的百分比为15%,每天参加体育锻炼的时间不足60min的有30人;
(2)被调查的学生总数为120人,统计表中m的值为42,统计图中n的值为25,被调查学生每天参加体育锻炼时间的中位数落在C组;
(3)该校共有960名学生,根据调查结果,估计该校每天参加体育锻炼的时间不少于60min的学生数.
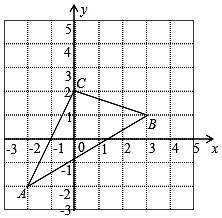 如图,△ABC在直角坐标系中
如图,△ABC在直角坐标系中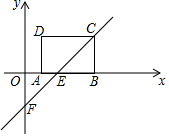 如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.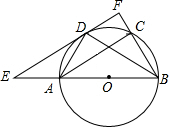 如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5.
如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).