题目内容
20. 已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,求证:∠A=90°.
已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,求证:∠A=90°.
分析 连接CE,由线段垂直平分线的性质得出CE=BE,再由已知条件得出AE2+AC2=CE2,由勾股定理的逆定理即可得出△ACE是直角三角形,∠A=90°.
解答 证明:连接CE,如图所示:
∵D是BC的中点,DE⊥BC,
∴CE=BE,
∵BE2-EA2=AC2,
∴CE2-EA2=AC2,
∴EA2+AC2=CE2,
∴△ACE是直角三角形,即∠A=90°.
点评 本题考查了线段垂直平分线的性质、勾股定理的逆定理;熟练掌握勾股定理的逆定理,并能进行推理论证是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.将一元二次方程3x2+4x=7化成一般式后,一次项系数和常数项分别为( )
| A. | 4,7 | B. | -4,7 | C. | 4,-7 | D. | -4,-7 |
11.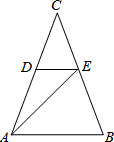 如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )
如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )
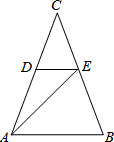 如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )
如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )| A. | 70° | B. | 65° | C. | 60° | D. | 55° |
8.下列命题中,真命题是( )
| A. | 两组数据1、2、3、4、5与21、22、23、24、25的离散程度相同 | |
| B. | 若点C是线段AB的黄金分割点,且AB=10,则AC≈6.18 | |
| C. | 等腰三角形的边长是方程x2-6x+8=0的两个解,则这个三角形的底边长为2或4 | |
| D. | 在平行光线的照射下,不同物体的物高与影长成比例 |
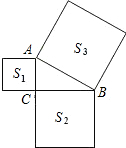 如图,在△ABC中,∠ACB=90°,以它的各边向外作三个正方形,面积分别是S1,S2,S3,已知S1=35,S3=100,则S2=65.
如图,在△ABC中,∠ACB=90°,以它的各边向外作三个正方形,面积分别是S1,S2,S3,已知S1=35,S3=100,则S2=65. 如图,每个小正方形的边长都为1,A、B、C是小正方形的顶点,则∠ABC=45°.
如图,每个小正方形的边长都为1,A、B、C是小正方形的顶点,则∠ABC=45°. 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连接AF,BF,则∠ABF的度数是30°.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连接AF,BF,则∠ABF的度数是30°. 某市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取A、B、C三根木柱,使得A、B之间的距离与A、C之间的距离相等,并测得BC长为24米,A到BC的距离为5米,如图所示.请你帮他们求出滴水湖的半径.
某市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取A、B、C三根木柱,使得A、B之间的距离与A、C之间的距离相等,并测得BC长为24米,A到BC的距离为5米,如图所示.请你帮他们求出滴水湖的半径.