题目内容
13．小王和小李一起加工同一种零件，小王每小时比小李多加工4个，结果在相同的时间里，小王加工160个零件，小李加工120个零件．求小王和小李每小时分别可加工多少个零件？（列方程解应用题）分析 设小李平均每小时加工x个零件，则小王平均每小时加工（x+4）个零件，根据“结果在相同的时间里，小王加工160个零件，小李加工120个零件”列出方程并解答，注意分式方程要验根．
解答 解：设小李平均每小时加工x个零件，小王平均每小时加工（x+4）个零件，则
$\frac{160}{x+4}$=$\frac{120}{x}$，
解得x=12，
经检验，x=12是原方程的根，
则x+4=16．
答：小李平均每小时加工12个零件，小王平均每小时加工16个零件．
点评 本题考查了分式方程的应用．利用分式方程解应用题时，一般题目中会有两个相等关系，这时要根据题目所要解决的问题，选择其中的一个相等关系作为列方程的依据，而另一个则用来设未知数．
练习册系列答案
相关题目
3．我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆．若在△ABC中，AB=AC，BC=6，∠BAC=120°，则△ABC的最小覆盖圆的半径是（ ）
| A． | 3 | B． | $2\sqrt{3}$ | C． | 2 | D． | $3\sqrt{3}$ |
4．
如图，笑脸盖住的点的坐标可能为（ ）
如图，笑脸盖住的点的坐标可能为（ ）| A． | （5，2） | B． | （3，-4） | C． | （-4，-6） | D． | （-1，3） |
1．关于x的方程-ax=b（a≠0）的解是（ ）
| A． | x=$\frac{b}{a}$ | B． | x=-$\frac{b}{a}$ | C． | x=-$\frac{a}{b}$ | D． | x=$\frac{a}{b}$ |
18．式子（x-3）0+$\sqrt{x}$有意义，则x的取值范围是（ ）
| A． | x≠3 | B． | x≥0 | C． | x≠3或x≥0 | D． | x≠3且x≥0 |
2．
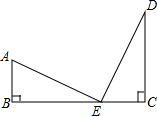如图所示，Rt△ABE≌Rt△ECD，点B、E、C在同一直线上，则结论：①AE=ED；②AE⊥DE；③BC=AB+CD；④AB∥DC中成立的是（ ）
如图所示，Rt△ABE≌Rt△ECD，点B、E、C在同一直线上，则结论：①AE=ED；②AE⊥DE；③BC=AB+CD；④AB∥DC中成立的是（ ）| A． | 仅① | B． | 仅①③ | C． | 仅①③④ | D． | 仅①②③④ |
3．下面计算正确的（ ）
| A． | 3x2-x2=3 | B． | a+b=ab | C． | 3+x=3x | D． | -ab+ba=0 |