题目内容
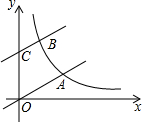 如图,直线y=
如图,直线y=| 1 |
| 2 |
| k |
| x |
| 1 |
| 2 |
| k |
| x |
| A、(2,3) | ||||
| B、(2,4) | ||||
C、(1,
| ||||
D、(
|
考点:反比例函数与一次函数的交点问题,一次函数图象与几何变换
专题:
分析:分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,CF⊥BE于F,再设A(2a,a),由于OA=2BC,得出B(a,
a+2),再根据反比例函数中k=xy为定值列出关于a的方程,解方程求出a的值,进而得到B点的坐标.
| 1 |
| 2 |
解答:解:分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,CF⊥BE于F,设A(2a,a),
∵OA=2BC,BC∥OA,CF∥x轴,
∴△BCF∽△AOD,
∴CF=
OD=a,
∵点B在直线y=
x+2上,
∴B(a,
a+2),
∵点A、B在双曲线y=
上,
∴2a•a=a•(
a+2),解得a=
,
∴
a+2=
×
+2=
,
∴B点的坐标为(
,
).
故选D.
∵OA=2BC,BC∥OA,CF∥x轴,

∴△BCF∽△AOD,
∴CF=
| 1 |
| 2 |
∵点B在直线y=
| 1 |
| 2 |
∴B(a,
| 1 |
| 2 |
∵点A、B在双曲线y=
| k |
| x |
∴2a•a=a•(
| 1 |
| 2 |
| 4 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 8 |
| 3 |
∴B点的坐标为(
| 4 |
| 3 |
| 8 |
| 3 |
故选D.
点评:本题考查的是反比例函数与一次函数的交点问题,一次函数图象与几何变换,根据题意作出辅助线,设出A、B两点的坐标,再根据k=xy为定值列出方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
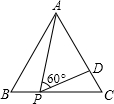 如图,如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是( )
如图,如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是( )A、
| ||
B、
| ||
C、
| ||
D、
|
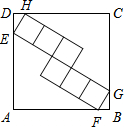 如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为
如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为 两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为
两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为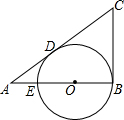 已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( )
已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( ) 如图,已知DE∥BC,且∠ADE=62°,∠DEC=112°,则∠B=
如图,已知DE∥BC,且∠ADE=62°,∠DEC=112°,则∠B= 在边长为1的小正方形网格中(如图),△AOB的顶点均在格点上
在边长为1的小正方形网格中(如图),△AOB的顶点均在格点上