题目内容
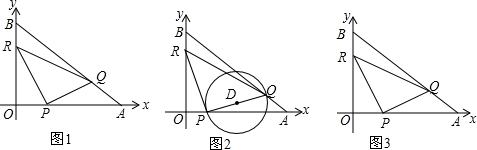
如图，在△ABC中，∠C=90°，∠BAC和∠ABC的角平分线交于点D，DE⊥BC于E，DF⊥AC于F．四边形CFDE是什么特殊四边形？证明你的结论．考点：正方形的判定
专题：
分析：首先利用垂直的定义证得四边形CFDE是矩形，然后利用角平分线的性质得到DE=DF，从而判定该四边形是正方形．
解答：解：四边形CFDE是正方形，
理由：∵∠C=90°，DE⊥BC于点E，DF⊥AC于点F，
∴四边形DECF为矩形，
∵∠A、∠B的平分线交于点D，
∴DF=DE，
∴四边形CFDE是正方形．
理由：∵∠C=90°，DE⊥BC于点E，DF⊥AC于点F，
∴四边形DECF为矩形，
∵∠A、∠B的平分线交于点D，
∴DF=DE，
∴四边形CFDE是正方形．
点评：本题主要考查了角平分线的性质，三角形的内切圆与内心，解题的关键是利用正方形的判定方法证得四边形CFDE是正方形．
练习册系列答案
相关题目
在函数①y=
x；②y=
；③y=
；④y=x2+1中，y是x的一次函数有（ ）
| 1 |
| 2 |
| 1 |
| x |
| x-1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，已知⊙O的直径AB垂直于弦CD于E，连结AD，BD，OC，OD，且OD=5．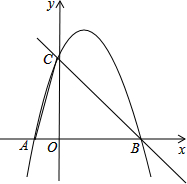
如图，在平面直角坐标系中，点O为坐标原点，直线y=-x+n与x轴、y轴分别交于B、C两点，抛物线y=ax2+bx+3（a≠0）过C、B两点，交x轴于另一点A，连接AC，且tan∠CAO=3．点P是线段CB上一点（不和B、C重合），过点P作x轴的垂线，垂足为H，交抛物线于Q，
如图，AB∥CD，∠A=40°，∠C=45°，求∠D和∠AOC．
如图，在折成ABCDEF中，已知∠1=∠2=∠3=∠4=∠5，延长AB、GF交于点M，试探索∠M与∠3的关系，说明理由．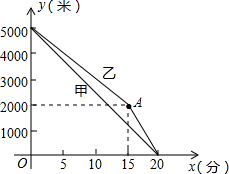
甲、乙两名运动员进行长跑训练，两人距离终点的路程y（米）与跑步时间x（分）之间的关系如图所示，根据图象回答下列问题：