题目内容
9．
如图，在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AB于点E，若EA=2，则BE=（ ）| A． | 3 | B． | 4 | C． | 6 | D． | 8 |
分析 根据在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AB于点E，EA=2，可以求得AD⊥BC，∠B=∠C，以及∠B和∠C的度数，从而可以求得AD、AB的长，从而可以求得BE的长，本题得以解决．
解答 解：∵在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，
∴AD⊥BC，∠B=∠C=30°，
∴∠ADC=90°，
∵DE⊥AB于点E，EA=2，
∴∠DEA=90°，∠DEB=90°，
∴∠BAD=60°，∠EDA=30°，
∴AD=2AE=4，
∴AB=2AD=8，
∴BE=AB-AE=8-2=6，
故选C．
点评 本题考查含30度角的直角三角形和等腰三角形的性质，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
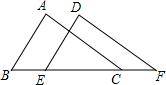如图，在△ABC和△DEF，若AB=DE，BE=CF，要使△ABC≌△DEF，还需添加一个条件（只要写出一个就可以）是∠B=∠DEF．
如图，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD与BE相交于点F，连接ED．
14．
边长分别为a和2a的两个正方形按如图的样式摆放并连线，则图中阴影部分的面积为（ ）
边长分别为a和2a的两个正方形按如图的样式摆放并连线，则图中阴影部分的面积为（ ）| A． | 3a2 | B． | $\frac{7}{4}{a}^{2}$ | C． | 2a2 | D． | $\frac{3}{2}{a}^{2}$ |
