题目内容
4. 如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接ED.
如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接ED.(1)求证:△BFD∽△ACD;
(2)再写出图中的两对相似三角形(不添加其它线段,不要求证明).
分析 (1)根据垂直得出∠BEC=90°,∠BDF=∠AEF=90°,∠ADC=90°,求出∠CBE=∠DAC,根据相似三角形的判定定理得出即可;
(2)根据相似三角形的判定定理判断即可.
解答 (1)证明:∵AD⊥BC,BE⊥AC,
∴∠BEC=90°,∠BDF=∠AEF=90°,∠ADC=90°,
∴∠CBE+∠C=90°,∠DAC+∠C=90°,
∴∠CBE=∠DAC,
又∵∠BDF=∠ADC=90°,
∴△BFD∽△ACD;
(2)解:△BFD∽△ACD,△ACD∽△BCE.
点评 本题考查了相似三角形的判定和性质的应用,能熟练地运用定理进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12. 如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )
如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )
 如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )
如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )| A. | 11° | B. | 35° | C. | 55° | D. | 70° |
16. 一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上,是图中数轴上的哪个点( )
一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上,是图中数轴上的哪个点( )
 一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上,是图中数轴上的哪个点( )
一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上,是图中数轴上的哪个点( )| A. | D点 | B. | C点 | C. | B点 | D. | A点 |
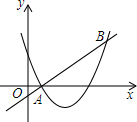 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3. 如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结AD,CD.则△ABC≌△ADC的依据是SSS.
如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结AD,CD.则△ABC≌△ADC的依据是SSS. 如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于点E,若EA=2,则BE=( )
如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于点E,若EA=2,则BE=( )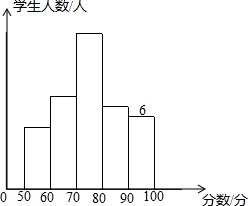 某校同学参加语文知识竞赛,将学生的成绩,进行整理后分成5组,绘制成频数分布直方图如下,图中从左到右各小组的频率分别是0.0625,0.25,0.375,0.1875,0.125且已知最右边小组的频数为6,结合直方图提供的信息,解答下列问题:
某校同学参加语文知识竞赛,将学生的成绩,进行整理后分成5组,绘制成频数分布直方图如下,图中从左到右各小组的频率分别是0.0625,0.25,0.375,0.1875,0.125且已知最右边小组的频数为6,结合直方图提供的信息,解答下列问题: