题目内容
1．（1）解方程：2x2+x-15=0（2）计算：sin30°-$\sqrt{2}$sin45°+tan60°-cos30°+20160．
分析 （1）先分解因式，即可得出两个一元一次方程，求出方程的解即可；
（2）先把各个角的函数值代入，再求出即可．
解答 解：（1）2x2+x-15=0，
（2x-5）（x+3）=0，
2x-5=0，x+3=0，
x1=$\frac{5}{2}$，x2=-3；
（2）原式=$\frac{1}{2}$-$\sqrt{2}$×$\frac{\sqrt{2}}{2}$+$\sqrt{3}$-$\frac{\sqrt{3}}{2}$+1
=$\frac{\sqrt{3}+1}{2}$．
点评 本题考查了解一元二次方程和特殊角的三角函数值的应用，能熟记解一元二次方程的解题思路和熟记特殊角的三角函数值是解此题的关键．
练习册系列答案
走进文言文系列答案
相关题目
12．
如图，?ABCD中，∠C=110°，BE平分∠ABC，则∠AEB等于（ ）
如图，?ABCD中，∠C=110°，BE平分∠ABC，则∠AEB等于（ ）| A． | 11° | B． | 35° | C． | 55° | D． | 70° |
如图，在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AB于点E，若EA=2，则BE=（ ）
16．
一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上，是图中数轴上的哪个点（ ）
一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上，是图中数轴上的哪个点（ ）| A． | D点 | B． | C点 | C． | B点 | D． | A点 |
6．
a、b在数轴上位置如图所示，则|a-b|等于（ ）
a、b在数轴上位置如图所示，则|a-b|等于（ ）| A． | -b-a | B． | a-b | C． | a+b | D． | -a+b |
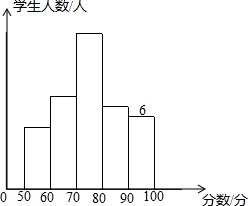某校同学参加语文知识竞赛，将学生的成绩，进行整理后分成5组，绘制成频数分布直方图如下，图中从左到右各小组的频率分别是0.0625，0.25，0.375，0.1875，0.125且已知最右边小组的频数为6，结合直方图提供的信息，解答下列问题：
如图，△ABC中，∠C=90°，∠A=30°．