题目内容
11．
已知正六边形ABCDEF，如图所示，其外接圆的半径是a，求正六边形的周长和面积．
分析 根据正六边形的半径等于边长即可得出正六边形的周长，再由三角函数求出边心距，即可求出正六边形的面积．
解答 解：∵正六边形的半径等于边长，
∴正六边形的边长AB=OA=a；
正六边形的周长=6AB=6a；
∵OM=OA•sin60°=$\frac{\sqrt{3}}{2}$a，
正六边形的面积S=6×$\frac{1}{2}$×a×$\frac{\sqrt{3}}{2}$a=$\frac{3\sqrt{3}}{2}$a2．
点评 本题考查的是正六边形的性质、三角函数、三角形面积的计算，解答此题的关键是熟知正六边形的边长等于半径．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6．
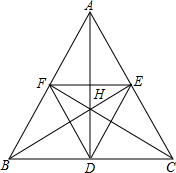如图，锐角△ABC的垂心为H，三条高的垂足分为D、E、F，则H是△DEF的（ ）
如图，锐角△ABC的垂心为H，三条高的垂足分为D、E、F，则H是△DEF的（ ）| A． | 垂心 | B． | 重心 | C． | 内心 | D． | 外心 |
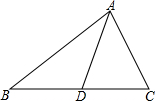如图，在△ABC中，点D是BC边的中点，已知AB=8cm，AC=6cm，△ABC的面积是12cm2．