题目内容
11.解方程组:$\left\{\begin{array}{l}{{x}^{2}-2xy+3{y}^{2}=9,①}\\{2{x}^{2}-xy+{y}^{2}=4.②}\end{array}\right.$.分析 根据解高次方程的方法可以求得方程组的解.
解答 解:$\left\{\begin{array}{l}{{x}^{2}-2xy+3{y}^{2}=9,①}\\{2{x}^{2}-xy+{y}^{2}=4.②}\end{array}\right.$,
①×4,得
4x2-8xy+12y2=36,③
②×9,得
18x2-9xy+9y2=36,④
④-③,得
14x2-xy-3y2=0,
∴(2x-y)(7x+3y)=0,
∴2x-y=0或7x+3y=0,
解得,y=2x或y=$-\frac{7x}{3}$,
将y=2x代入①,得
x2-2x×2x+3×(2x)2=0,
解得,x=±1,
当x=1时,y=2,当x=-1时,y=-2;
将y=$-\frac{7x}{3}$代入①,得
x=$±\frac{3\sqrt{22}}{22}$,
当x=$-\frac{3\sqrt{22}}{22}$时,y=$\frac{7\sqrt{22}}{22}$,
当x=$\frac{3\sqrt{22}}{22}$时,y=$-\frac{7\sqrt{22}}{22}$;
由上可得,原方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,$\left\{\begin{array}{l}{x=-\frac{3\sqrt{22}}{22}}\\{y=\frac{7\sqrt{22}}{22}}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{3\sqrt{22}}{22}}\\{y=-\frac{7\sqrt{22}}{22}}\end{array}\right.$.
点评 本题考查高次方程,解答本题的关键是明确解高次方程的方法.

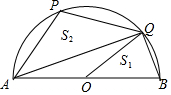 如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
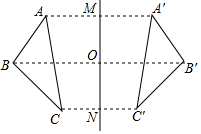 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )| A. | AC=A′C′ | B. | BO=B′O | C. | AA′⊥MN | D. | AB∥B′C′ |
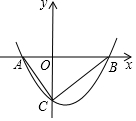 平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.
平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”. 如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数).
如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数).