题目内容
14.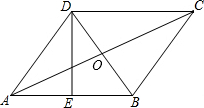 菱形ABCD中,对角线AC和BD相交于O,已知AC=8,BD=6,求AB边上的高.
菱形ABCD中,对角线AC和BD相交于O,已知AC=8,BD=6,求AB边上的高.
分析 首先利用菱形的性质得出AB的长,再利用菱形面积求法得出DE的长.
解答 解:∵菱形ABCD中,对角线AC和BD相交于O,AC=8,BD=6,
∴AO=4,BO=3,∠AOB=90°,
∴AB=5,
∴$\frac{1}{2}$×6×8=DE×AB,
解得:DE=$\frac{24}{5}$,
即AB边上的高为:$\frac{24}{5}$.
点评 此题主要考查了菱形的性质以及勾股定理,根据菱形的面积求出DE的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知直线l平行于直线y=-2x,且过点(4,5),则l的解析式为( )
| A. | y=2x+13 | B. | y=2x-13 | C. | y=-2x+13 | D. | y=-2x-13 |
4.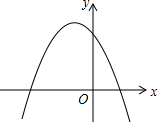 函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
 函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个同号的实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
 在Rt△ABC中,∠C=90°,∠B=2∠A,求∠B,∠A的度数.
在Rt△ABC中,∠C=90°,∠B=2∠A,求∠B,∠A的度数.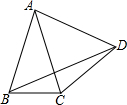 如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.
如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.
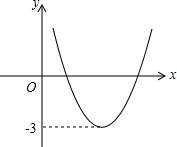 如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是有两个同号不等实数根.
如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是有两个同号不等实数根.