��Ŀ����
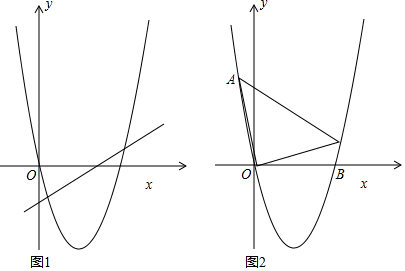
1��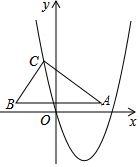 ��ͼ����ƽ��ֱ������ϵxOy�У�Rt��ABC��ֱ�Ƕ���C��������y=ax2+bx���˶���б��AB��ֱ��y�ᣬ��AB=8����ABC=60�㣬��Rt��ABC��б��AB����x����ʱ��B�������ǣ�-3��0����A��ǡ��������y=ax2+bx��
��ͼ����ƽ��ֱ������ϵxOy�У�Rt��ABC��ֱ�Ƕ���C��������y=ax2+bx���˶���б��AB��ֱ��y�ᣬ��AB=8����ABC=60�㣬��Rt��ABC��б��AB����x����ʱ��B�������ǣ�-3��0����A��ǡ��������y=ax2+bx����1����AB���ϵĸ���CD�ij���
��2���������߽���ʽ��
��3��Rt��ABC���˶��������п��ܱ�y��ֳ������֣����������ֵ����֮��Ϊ1��2ʱ����C�����꣮
���� ��1������ֱ������������ǻ��������A=��BCD=30�㣬Ȼ�����ֱ��������30������Ե�ֱ�DZߵ���б�ߵ�һ�����BC��BD�������ù��ɶ�����ʽ���㼴�ɵý⣻
��2�����ݵ�B�������AB�ij��������A�����꣬�������C�����꣬Ȼ�����ô���ϵ��������κ�������ʽ���
��3����AC��AB��y��Ľ���ֱ�ΪE��F���ٷ��������������������AEF��������AF���ٱ�ʾ��DF���õ���C�ĺ����꣬�ٸ��ݵ�C���������ϣ��ѵ�C�ĺ�����������������õ���C�������꼴�ɵý⣮
���  �⣺��1������C��CD��AB��D��
�⣺��1������C��CD��AB��D��
��Rt��ABC�У�AB=8����ABC=60�㣬
���A=30�㣬
��BC=$\frac{1}{2}$AB=4��AC=4$\sqrt{3}$��
��Rt��BCD�У���ABC=60�㣬
���ABC=60�㣬
���BCD=30�㣬
��BC=4��
��BD=2��CD=2$\sqrt{3}$��
����AB���ϵĸ���CD�ij�Ϊ2$\sqrt{3}$��
��2���ɣ�1��֪��BD=2��
��AB=8��B��-3��0����
��A��5��0����
��C�ĺ�����Ϊ-1��
��C��-1��2$\sqrt{3}$����
��A��5��0����C��-1��2$\sqrt{3}$��ǡ��������y=ax2+bx�ϣ�
��$\left\{\begin{array}{l}{25a+5b=0}\\{a-b=2\sqrt{3}}\end{array}\right.$��
��$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=-\frac{5\sqrt{3}}{3}}\end{array}\right.$��
�������߽���ʽΪy=$\frac{\sqrt{3}}{3}{x}^{2}-\frac{5\sqrt{3}}{3}x$��
��3���ɣ�1��֪��BC=4��AC=4$\sqrt{3}$��
��S��ABC=$\frac{1}{2}$BC•AC=8$\sqrt{3}$��
��$\frac{1}{3}$S��ABC=$\frac{8\sqrt{3}}{3}$��
�ɣ�1��֪��BD=2��CD=2$\sqrt{3}$��
��S��BCD=$\frac{1}{2}$BD•CD=2$\sqrt{3}$��
��$\frac{1}{3}$S��ABC��S��BCD��
��Rt��ABC���˶��������п��ܱ�y��ֳ������֣����������ֵ����֮��Ϊ1��2ʱ��y��ֻ�ܺ�AC��AB�ཻ�����ABC�ı�AC��AB��y���ཻ��E��F��
��Rt��AEF�У���A=30�㣬
��EF=AFtan30��=$\frac{\sqrt{3}}{3}$AF��
��S��AEF=$\frac{1}{2}$AF•EF=$\frac{\sqrt{3}}{6}$AF2��
�ٵ�S��AEF=$\frac{1}{3}$S��ABC=$\frac{8\sqrt{3}}{3}$��
��$\frac{\sqrt{3}}{6}$AF2=$\frac{8\sqrt{3}}{3}$��
��AF=4��
��AD=AB-BD=6��
��C��ĺ�����Ϊ-2��
�ߵ�C��������y=$\frac{\sqrt{3}}{3}{x}^{2}-\frac{5\sqrt{3}}{3}x$�ϣ�
���C��������Ϊ$\frac{\sqrt{3}}{3}��4-\frac{5\sqrt{3}}{3}����-2��$=$\frac{14\sqrt{3}}{3}$��
��C��-2��$\frac{14\sqrt{3}}{3}$����
�ڵ�S��AEF=$\frac{2}{3}$S��ABC=$\frac{16\sqrt{3}}{3}$��
��$\frac{\sqrt{3}}{6}$AF2=$\frac{16\sqrt{3}}{3}$��
��AF=4$\sqrt{2}$��
��AD=AB-BD=6��
��C��ĺ�����Ϊ4$\sqrt{2}$-6��
�ߵ�C��������y=$\frac{\sqrt{3}}{3}{x}^{2}-\frac{5\sqrt{3}}{3}x$�ϣ�
���C��������Ϊ$\frac{\sqrt{3}}{3}����4\sqrt{2}-6��^{2}-\frac{5\sqrt{3}}{3}��4\sqrt{2}-6��$=$\frac{98\sqrt{3}-68\sqrt{6}}{3}$��
��C��4$\sqrt{2}$-6��$\frac{98\sqrt{3}-68\sqrt{6}}{3}$����
�������������ĵ�C������Ϊ$��{-2\;��\;\;\frac{{14\sqrt{3}}}{3}}��$��$��{4\sqrt{2}-6\;��\;\;\frac{{98\sqrt{3}}}{3}-\frac{{68\sqrt{6}}}{3}}��$��
���� �����Ƕ��κ����ۺ����ͣ���Ҫ������ֱ������������ǻ�������ʣ����ɶ�����Ӧ�ã�����ϵ��������κ�������ʽ�����κ���ͼ���ϵ��������������2����ʾ����C�ĺ������ǽ���Ĺؼ�����3���ѵ��������������ε���������A��y��ľ��룬��AF�ij��ȣ�

| A�� | 6x6��2x2=3x2 | B�� | 8x8��4x2=2x6 | C�� | a3��a3=0 | D�� | $\frac{2}{3}$a5b��$\frac{3}{2}$a5b=1 |
| A�� | xy��0 | B�� | $\frac{x}{y}$��0 | C�� | x+y��0 | D�� | x-y��0 |
| A�� | ��A+��B=180�� | B�� | ��B+��D=180�� | C�� | ��B+��C=180�� | D�� | ��A+��B=180�� |

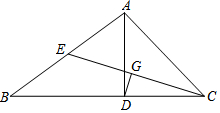 ��֪����ͼ���ڡ�ABC�У�AD��BC���ϵĸߣ���B=30�㣬��ACB=45�㣬CE��AB���ϵ����ߣ�
��֪����ͼ���ڡ�ABC�У�AD��BC���ϵĸߣ���B=30�㣬��ACB=45�㣬CE��AB���ϵ����ߣ�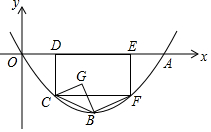 ��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{1}{2}$ax2-2ax��a��0����x�������ύ�ڵ�A����B�������ߵĶ��㣬����CDEF�Ķ���D��E��x�������ϣ�C��F���������ϣ��ҵ�D�ĺ�����Ϊ1������BC��BF����BCΪб�����Ҳ�������ֱ��������BCG
��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{1}{2}$ax2-2ax��a��0����x�������ύ�ڵ�A����B�������ߵĶ��㣬����CDEF�Ķ���D��E��x�������ϣ�C��F���������ϣ��ҵ�D�ĺ�����Ϊ1������BC��BF����BCΪб�����Ҳ�������ֱ��������BCG