题目内容
15．
如图，五角星绕着它的旋转中心旋转，使得△ABC与△DEF重合，那么旋转角的度数至少为（ ）| A． | 60° | B． | 120° | C． | 72° | D． | 144° |
分析 由于五角星的五个角可组成正五边形，根据正五边形的性质得到正五边形的中心角为72°，然后可判断要使△ABC与△DEF重合，旋转角的度数至少为2个72°．
解答 解：五角星的五个角可组成正五边形，而正五边形的中心角为$\frac{360°}{5}$=72°，
所以五角星绕着它的旋转中心至少顺时针旋转2个72°，使得△ABC与△DEF重合．
故选D．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正五边形的性质．
练习册系列答案
阅读快车系列答案
相关题目
19．在Rt△ABC中，∠C=90°，下列式子正确的是（ ）
| A． | sinA+cosA＜1 | B． | sinA+cosA=1 | C． | sinA+cosA＞1 | D． | sinA+cosA≥1 |
3．如图，已知1号、4号两个正方形的面积和为7，2号、3号两个正方形的面积和为5，则a，c这2个方形的面积和为（ ）
| A． | 10 | B． | 15 | C． | 22 | D． | 12 |
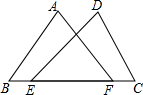如图，点E，F在BC边上，AB=DC，∠B=∠C．要使得∠A=∠D．则可以添加的条件是∠AFE=∠DEF或BF=CE或BE=CF（答案不唯一）（写一个即可）．
5．
如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离OE=3cm，则⊙O的半径为（ ）
如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离OE=3cm，则⊙O的半径为（ ）| A． | 2cm | B． | 3cm | C． | 5cm | D． | 10cm |