题目内容
已知：如图，E、F是?ABCD的对角线AC上的两点，CE=AF．请你猜想：线段BE与线段DF有怎样的关系？并对你的猜想加以证明．考点：平行四边形的性质,全等三角形的判定与性质
专题：
分析：首先连接BD交AC于点O，由?ABCD的对角线AC上的两点，CE=AF，易得OE=OF，OB=OD，继而可得四边形BEDF是平行四边形，即可证得结论．
解答：
解：BE=DF，BE∥DF．
证明：连接BD交AC于点O，
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵CE=AF，
∴CE-OC=AF-OA，
即OE=OF，
∴四边形BEDF是平行四边形，
∴BE=DF，BE∥DF．
解：BE=DF，BE∥DF．证明：连接BD交AC于点O，
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵CE=AF，
∴CE-OC=AF-OA，
即OE=OF，
∴四边形BEDF是平行四边形，
∴BE=DF，BE∥DF．
点评：此题考查了平行四边形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，在△ABC中，∠ACB=90°，∠A=30°，将△ABC绕点C按顺时针方向旋转n度后，得到△EDC，使点D刚好落在斜边AB上，则n的大小为（ ）
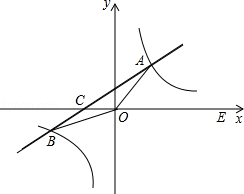如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数y=的图象交于一、三象限内的A、B两点，直线AB与x轴交于点C，点B的坐标为（-6，n），线段OA=5，E为x轴正半轴上一点，且tan∠AOE=