题目内容
13. 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC,其中∠AEB=24°,AB=4cm.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC,其中∠AEB=24°,AB=4cm.(1)求∠ACB的度数;
(2)线段BE和EC有怎样的关系,请说明理由;
(3)求△ABE的面积.
分析 (1)首先证明△EBC是等腰直角三角形,推出∠EAO=∠CBO=45°,利用“8字型”推出∠BCO=∠AEB=24°.
(2)结论:EB=EC.见(1)中证明;
(3)作EH⊥AD于H.根据S△ABE=S△EDC=$\frac{1}{2}$•CD•EH,计算即可;
解答 (1)解:∵△AED是直角三角形,∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC-∠EDA=180°-45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=$\frac{1}{2}$AC,
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中
$\left\{\begin{array}{l}{AE=DE}\\{∠EAB=∠EDC}\\{AB=DC}\end{array}\right.$,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°,
∴△EBC是等腰直角三角形,
∴∠EAD=∠EBC=45°,设BE交AD于O,
∵∠AOE=∠BOC,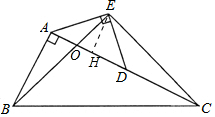
∴∠AEO=∠BCO=24°.
(2)结论:BE=EC.
见(1)中证明.
(3)作EH⊥AD于H.
∵AB=AD=DC=4,△AED是等腰直角三角形,
∴EH=$\frac{1}{2}$AD=2,
∵△EAB≌△EDC,
∴S△ABE=S△EDC=$\frac{1}{2}$•CD•EH=$\frac{1}{2}$×4×2=4.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

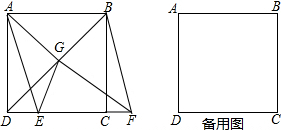
| A. | 如果增加条件AC=A′C′,那么△ABC≌△A′B′C′(SAS) | |
| B. | 如果增加条件BC=B′C′,那么△ABC≌△A′B′C′(SAS) | |
| C. | 如果增加条件∠B=∠B′,那么△ABC≌△A′B′C′(ASA) | |
| D. | 如果增加条件∠C=∠C′,那么△ABC≌△A′B′C′(AAS) |
| 购苹果数 | 不超过30kg | 30kg以下但不超过50kg | 50kg以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
(2)甲班第一次,第二次分别购买苹果多少千克?
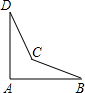 如图,∠BAD=90°,∠ADC=30°,∠BCD=142°,求∠B的度数.
如图,∠BAD=90°,∠ADC=30°,∠BCD=142°,求∠B的度数.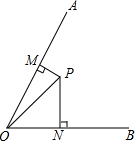 如图,∠AOB=60°,P为∠AOB内一点,P到OA、OB的距离PM、PN分别为2和11,求OP的长.
如图,∠AOB=60°,P为∠AOB内一点,P到OA、OB的距离PM、PN分别为2和11,求OP的长.