题目内容
8.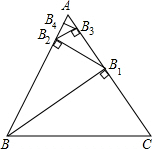 如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,…,Bn-1Bn是△ABn-2Bn-1的高,则Bn-1Bn的长是$\frac{\sqrt{3}}{{2}^{n}}$.
如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,…,Bn-1Bn是△ABn-2Bn-1的高,则Bn-1Bn的长是$\frac{\sqrt{3}}{{2}^{n}}$.
分析 根据等边三角形性质得出AB1=CB1=$\frac{1}{2}$,∠AB1B=∠BB1C=90°,由勾股定理求出BB1=$\frac{\sqrt{3}}{2}$,求出△ABC的面积是$\frac{\sqrt{3}}{4}$;求出S${\;}_{△AB{B}_{1}}$=S${\;}_{△BC{B}_{1}}$=$\frac{\sqrt{3}}{8}$,根据三角形的面积公式求出B1B2=$\frac{\sqrt{3}}{4}$,由勾股定理求出BB2,根据S${\;}_{△AB{B}_{1}}$=S${\;}_{△B{B}_{1}{B}_{2}}$+S${\;}_{△A{B}_{2}{B}_{1}}$代入求出B2B3=$\frac{\sqrt{3}}{8}$=$\frac{\sqrt{3}}{{2}^{3}}$,B3B4=$\frac{\sqrt{3}}{{2}^{4}}$,B4B5=$\frac{\sqrt{3}}{{2}^{5}}$,推出Bn-1Bn=$\frac{\sqrt{3}}{{2}^{n}}$.
解答 解:∵△ABC是等边三角形,
∴BA=AC,
∵BB1是△ABC的高,
∴AB1=CB1=$\frac{1}{2}$,∠AB1B=∠BB1C=90°,
由勾股定理得:BB1=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$;
∴△ABC的面积是$\frac{1}{2}×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$;
∴S${\;}_{△AB{B}_{1}}$=S${\;}_{△BC{B}_{1}}$=$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{8}$,
∴$\frac{\sqrt{3}}{8}$=$\frac{1}{2}$×1×B1B2,
B1B2=$\frac{\sqrt{3}}{4}$,
由勾股定理得:BB2=$\sqrt{(\frac{\sqrt{3}}{2})^{2}-(\frac{\sqrt{3}}{4})^{2}}$=$\frac{3}{4}$,
∵S${\;}_{△AB{B}_{1}}$=S${\;}_{△B{B}_{1}{B}_{2}}$+S${\;}_{△A{B}_{2}{B}_{1}}$,
∴$\frac{\sqrt{3}}{8}$=$\frac{1}{2}×\frac{3}{4}×\frac{\sqrt{3}}{4}$+$\frac{1}{2}×\frac{1}{2}$×B2B3,
B2B3=$\frac{\sqrt{3}}{8}$,
B3B4=$\frac{\sqrt{3}}{16}$,
B4B5=$\frac{\sqrt{3}}{32}$,
…,
Bn-1Bn=$\frac{\sqrt{3}}{{2}^{n}}$.
故答案为:$\frac{\sqrt{3}}{{2}^{n}}$.
点评 本题考查了等边三角形的性质,勾股定理,三角形的面积等知识点的应用,关键是能根据计算结果得出规律.

| A. | m=-2 | B. | m=2 | C. | m=1 | D. | m=1或m=2 |
| A. | 4 | B. | 0 | C. | 1 | D. | 2 |
 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.