题目内容
20. 如图,AB∥CD,AB∥MN.
如图,AB∥CD,AB∥MN.(1)请问CD与MN是否平行?试说明理由;
(2)试判断∠BEF,∠EFG,∠FGD之间的关系,并说明理由;
(3)若∠AEF=150°,∠DGF=60°,试判断EF和GF的位置关系,并说明理由.
分析 (1)根据平行公理的推论即可得到结论;
(2)由平行线的性质可得AB∥MN∥CD,由两直线平行,内错角相等,得到∠BEF=∠EFM,∠FGD=∠MFG,于是得到∠BEF+∠FGD=∠EFM+∠MFG,即可得到结论;
(3)思路同(2)根据∠EFG=∠FGD+∠BEF,求出∠EFG=90°从而得出EF⊥FG.
解答 (1)证明:∵AB∥CD,AB∥MN,
∴CD∥MN;
(2)解:∠EFG=∠FGD+∠BEF,
理由:∵AB∥CD,AB∥MN,
∴CD∥MN,
∴∠BEF=∠EFM,
∵CD∥MN,
∴∠FGD=∠MFG
∴∠BEF+∠FGD=∠EFM+∠HFG,
即:∠BEF+∠FGD=∠EFG,
∴∠EFG=∠FGD+∠BEF;
(3)EF⊥FG,理由:
解:∵AB∥CD,AB∥MN
∴CD∥MN,
∵∠AEF+∠BEF=180°(平角的定义)
∴∠BEF=180°-∠AEF=180°-150°=30°,
∵AB∥MN,
∴∠BEF=∠EFM,
∵CD∥MN,
∴∠FGD=∠MFG,
∴∠BEF+∠FGD=∠EFH+∠HFG,
即:∠BEF+∠FGD=∠EFG,
∴∠EFG=∠FGD+∠BEF=60°+30°=90°,
∴EF⊥FG.
点评 本题考查了平行线的性质和判定的应用,能运用定理进行推理是解此题的关键,注意:①同位角相等,两直线平行,②内错角相等,两直线平行,反之亦然.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
8.下列运算正确的是( )
| A. | x2+x3=x5 | B. | x4•x2=x6 | C. | (x2)3=x8 | D. | x6÷x2=x3 |
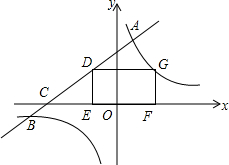 如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1.
如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1.