题目内容
1．若x1、x2是一元二次方程x2+3x-2=0的两个根，则x1+x2的值是（ ）| A． | 3 | B． | -3 | C． | 2 | D． | -2 |
分析 根据一元二次方程的根与系数的关系x1+x2=-$\frac{b}{a}$可以直接求得x1+x2的值．
解答 解：∵一元二次方程x2+3x-2=0的一次项系数是a=1，二次项系数b=3，
∴由韦达定理，得
x1+x2=-3．
故选B．
点评 此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
相关题目
11．
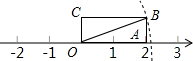如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（ ）
如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（ ）| A． | 2.5 | B． | 2$\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
12．若x1，x2是一元二次方程x2+ax+b=0的两个根，若x1•x2=-4，则（ ）
| A． | a=-4 | B． | a=4 | C． | b=-4 | D． | b=4 |
6．若x1、x2是一元二次方程x2-2x-5=0的两个根，则x1•x2的值是（ ）
| A． | 2 | B． | -2 | C． | 5 | D． | -5 |
如图，正方形ABCD边长为2，以直线AB为轴，将正方形旋转一周，所得圆柱的主视图（正视图）的周长是12．
10．在平面直角坐标系中，已知锐角α的顶点在原点，始边与x轴的正半轴重合，终边在第一象限内，且经过点P（3，4），则下列各式正确的是（ ）
| A． | sinα=$\frac{3}{5}$ | B． | sinα=$\frac{4}{5}$ | C． | sinα=$\frac{3}{4}$ | D． | sinα=$\frac{4}{3}$ |