题目内容
 如图,AB=8,以AB为直径的半圆绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是
如图,AB=8,以AB为直径的半圆绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是考点:扇形面积的计算,旋转的性质
专题:
分析:根据题意得出AB=AB′=8,∠BAB′=60°,根据图形得出图中阴影部分的面积S=
+
π×82-
π×82,求出即可.
| 60π×82 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:
∵AB=AB′=8,∠BAB′=60°
∴图中阴影部分的面积是:
S=S扇形B′AB+S半圆O′-S半圆O
=
+
π×82-
π×82
=
π.
故答案为:
π.

∵AB=AB′=8,∠BAB′=60°
∴图中阴影部分的面积是:
S=S扇形B′AB+S半圆O′-S半圆O
=
| 60π×82 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 32 |
| 3 |
故答案为:
| 32 |
| 3 |
点评:本题考查了旋转的性质,扇形的面积的应用,通过做此题培养了学生的计算能力和观察图形的能力,题目比较好,难度适中.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知
,则x-y的值是( )
|
| A、1 | B、-1 | C、3 | D、-3 |
若
=
,则( )
| x-3 |
| 15-2x |
| A、x=6 | B、x=5 |
| C、x=4 | D、x=3 |
已知
与
都是关于x、y的方程y=kx+b的解,则k与b的值分别为( )
|
|
| A、k=-2,b=8 |
| B、k=-2,b=0 |
| C、k=2,b=8 |
| D、k=2,b=-8 |
 如图,如果张力的位置可表示为(1,3),则王红的位置应表示为( )
如图,如果张力的位置可表示为(1,3),则王红的位置应表示为( )| A、(4,1) |
| B、(4,2) |
| C、(2,4) |
| D、(3,4) |
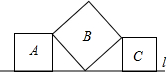 如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为
如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为 如图,AB∥CD∥EF,BC∥ED,∠E=110°,则∠B的度数是
如图,AB∥CD∥EF,BC∥ED,∠E=110°,则∠B的度数是