Question

【题目】如图,点在函数的图象上, 都是等腰直角三角形.斜边都在轴上(是大于或等于2的正整数),点的坐标是______．

Answer 1

【答案】

【解析】

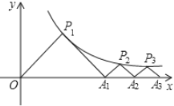
过点P1作P1E⊥x轴于点E，过点P2作P2F⊥x轴于点F，过点P3作P3G⊥x轴于点G，根据△P1OA1，△P2A1A2，△P3A2A3都是等腰直角三角形，可求出P1，P2，P3的坐标，从而总结出一般规律得出点Pn的坐标．

解：过点P1作P1E⊥x轴于点E，过点P2作P2F⊥x轴于点F，过点P3作P3G⊥x轴于点G，

∵△P1OA1是等腰直角三角形，

∴P1E=OE=A1E=OA1，

设点P1的坐标为（a，a），（a＞0），

将点P1（a，a）代入，可得a=1，

故点P1的坐标为（1，1），则OA1=2，

设点P2的坐标为（b+2，b），将点P2（b+2，b）代入，可得b=，

故点P2的坐标为（，），

则A1F=A2F=，OA2=OA1+A1A2=，

设点P3的坐标为（c+，c），将点P3（c+，c）代入，

可得c=，故点P3的坐标为（，），

综上可得：P1的坐标为（1，1），P2的坐标为（，），P3的坐标为（，），

总结规律可得：Pn坐标为；

故答案为：.